Physics (Grades 9–12)
Subtest 2 Sample Items
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Expand All | Collapse All
Question 1
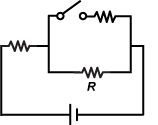
1. The diagram below shows a circuit consisting of a switch S and several resistors of resistance R.
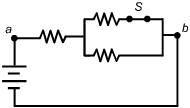
The upper left hand corner of the circuit is labeled point a. Starting at point a and traversing the circuit from left to right one encounters a single resistor. Next, one encounters two resistors in parallel. Of the two parallel resistors, the top resistor is in series with a switch labeled S. Continuing to the right along a single wire, one encounters the upper right hand corner, which is labeled point b. Continuing to traverse the circuit one encounters a battery before returning to point a.
Which of the following statements best describes what will happen if switch S is opened?
- The equivalent resistance of the circuit will decrease.
- The power supplied to the circuit will decrease.
- The current through the circuit will increase.
- The voltage across a and b will increase.
Answer to question 1
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0010) With the switch closed, the equivalent resistance of the circuit is RCLOSED = R + Req = 1.5R, since Req = 0.5R. When the switch is opened, the equivalent resistance of the circuit becomes ROPEN = R + R = 2R. So the equivalent resistance of the circuit increases when the switch is opened. Then, using
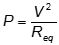 shows that the power supplied to the circuit must decrease when the switch is opened.
Correct Response: B. (Objective 0010) With the switch closed, the equivalent resistance of the circuit is R subscript CLOSED = R + R subscript eq = 1.5R, since R subscript e q = 0.5R. When the switch is opened, the equivalent resistance of the circuit becomes R subscript OPEN = R + R = 2R. So the equivalent resistance of the circuit increases when the switch is opened. Then, using P equals V squared over R subscript e
q shows that the power supplied to the circuit must decrease when the switch is opened.
shows that the power supplied to the circuit must decrease when the switch is opened.
Correct Response: B. (Objective 0010) With the switch closed, the equivalent resistance of the circuit is R subscript CLOSED = R + R subscript eq = 1.5R, since R subscript e q = 0.5R. When the switch is opened, the equivalent resistance of the circuit becomes R subscript OPEN = R + R = 2R. So the equivalent resistance of the circuit increases when the switch is opened. Then, using P equals V squared over R subscript e
q shows that the power supplied to the circuit must decrease when the switch is opened.
Question 2
2. A resistor connected across a constant voltage source dissipates power P. If the value of the resistance is doubled and the voltage remains the same, what is the power dissipated by the new resistor?
-
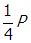
-
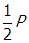
- 2P
- 4P
Answer to question 2
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0010) The power consumed by a device in an electric circuit is the product of the voltage and the current, or P = IV. For a resistor, V = IR, where R is the resistance (Ohm's law). Solving Ohm's law for current gives
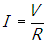 and by substitution,
and by substitution,
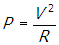 . Since the voltage remains constant, doubling the resistance will reduce the amount of power dissipated by Joule heating by a factor of one-half
. Since the voltage remains constant, doubling the resistance will reduce the amount of power dissipated by Joule heating by a factor of one-half
 . This is due to the fact that increasing the resistance will decrease the current, and therefore the power consumed.
Correct Response: B. (Objective 0010) The power consumed by a device in an electric circuit is the product of the voltage and the current, or P equals I V. For a resistor, V equals I R, where R is the resistance (Ohm's law). Solving Ohm's law for current gives I equals V over R and by substitution, P equals V squared over R. Since the voltage remains constant, doubling the resistance will reduce the amount of power dissipated by Joule heating by a factor of one-half, open parenthesis one-half P close parenthesis. This is due to the fact that increasing the resistance will decrease the current, and therefore the power consumed.
. This is due to the fact that increasing the resistance will decrease the current, and therefore the power consumed.
Correct Response: B. (Objective 0010) The power consumed by a device in an electric circuit is the product of the voltage and the current, or P equals I V. For a resistor, V equals I R, where R is the resistance (Ohm's law). Solving Ohm's law for current gives I equals V over R and by substitution, P equals V squared over R. Since the voltage remains constant, doubling the resistance will reduce the amount of power dissipated by Joule heating by a factor of one-half, open parenthesis one-half P close parenthesis. This is due to the fact that increasing the resistance will decrease the current, and therefore the power consumed.
Question 3
3. All of the resistors in the circuit below are identical and the battery is ideal.
The circuit diagram indicates a voltage source in series with a resistor and in series with two resistors that are in parallel. One of the two parallel resistors is in series with a switch.
Each resistor in the circuit has a value of 10 Ω. While the switch is open, a voltmeter placed across the resistor marked R reads 40 V. What is the current through the battery when the switch is closed?
- 1.3 A
- 2.6 A
- 3.9 A
- 5.3 A
Answer to question 3
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0010) When the switch is open, the circuit consists of two 10 Ω resistors in series, so each of the two resistors has the same current through it. Because the voltage across resistor R is 40 V, by V = IR the voltage across the other resistor is 40 V. By Kirchhoff's voltage law, 40 V + 40 V − Vbattery = 0.0 V, so the voltage across the battery is 80 V. When the switch is closed, the circuit consists of one resistor in series with a parallel circuit consisting of two resistors. The total resistance of the closed circuit is RT = 10 Ω + Req, where
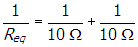 or Req = 5 Ω, and RT = 15 Ω. This circuit can be replaced with an equivalent circuit of resistance 15 Ω connected in series with an 80 V battery. From V = IR the current through the battery is 5.3 A.
Correct Response: D. (Objective 0010) When the switch is open, the circuit consists of two 10 Omega resistors in series, so each of the two resistors has the same current through it. Because the voltage across resistor R is 40 V, by V equals I R the voltage across the other resistor is 40 V. By Kirchhoff's voltage law, 40 V plus 40 V minus V subscript battery equals 0.0 V, so the voltage across the battery is 80 V. When the switch is closed, the circuit consists of one resistor in series with a parallel circuit consisting of two resistors. The total resistance of the closed circuit is R sub t equals 10 Omega plus R sub e q where one over r sub e q equals one over ten ohms plus one over ten ohms or R sub eq equals 5 Omega, and R sub t equals 15 Omega. This circuit can be replaced with an equivalent circuit of resistance 15 Omega connected in series with an 80 V battery. From V equals I R the current through the battery is 5.3 A.
or Req = 5 Ω, and RT = 15 Ω. This circuit can be replaced with an equivalent circuit of resistance 15 Ω connected in series with an 80 V battery. From V = IR the current through the battery is 5.3 A.
Correct Response: D. (Objective 0010) When the switch is open, the circuit consists of two 10 Omega resistors in series, so each of the two resistors has the same current through it. Because the voltage across resistor R is 40 V, by V equals I R the voltage across the other resistor is 40 V. By Kirchhoff's voltage law, 40 V plus 40 V minus V subscript battery equals 0.0 V, so the voltage across the battery is 80 V. When the switch is closed, the circuit consists of one resistor in series with a parallel circuit consisting of two resistors. The total resistance of the closed circuit is R sub t equals 10 Omega plus R sub e q where one over r sub e q equals one over ten ohms plus one over ten ohms or R sub eq equals 5 Omega, and R sub t equals 15 Omega. This circuit can be replaced with an equivalent circuit of resistance 15 Omega connected in series with an 80 V battery. From V equals I R the current through the battery is 5.3 A.
Question 4
4. A physics student has two 10 Ω resistors and two 20 pF capacitors. The student would like to build a circuit component that requires a time constant of τ = RC = 800 ps. Which of the following arrangements could be used?
-

-
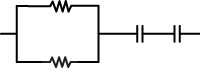
-
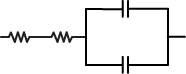
-
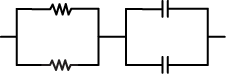
Answer to question 4
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0010) The time constant for a circuit consisting of capacitors and resistors is the product of the equivalent resistance and capacitance of the circuit. Answering the question requires determining the equivalent resistance and capacitance of each of the circuits. Analyzing each circuit requires using the formulas for two resistors and capacitors in series and parallel: Rs = R1 + R2,
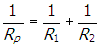 for resistors and
for resistors and
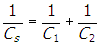 , Cp = C1 + C2 for capacitors. Applying these formulas to the circuit consisting of two resistors in series and two capacitors in parallel gives Rs = R1 + R2 = 10 Ω + 10 Ω = 20 Ω and Cp = C1 + C2 = 20 pF + 20 pF = 40 pF. The time constant is τ = RC = (20 Ω) (40 pF) = 800 ps.
Correct Response: C. (Objective 0010) The time constant for a circuit consisting of capacitors and resistors is the product of the equivalent resistance and capacitance of the circuit. Answering the question requires determining the equivalent resistance and capacitance of each of the circuits. Analyzing each circuit requires using the formulas for two resistors and capacitors in series and parallel: R subscript s equals R sub one plus R subscript two, one over r subscript p equals one over r subscript one baseline plus one over r subscript two for resistors and one over c subscript s equals one over c subscript one baseline plus one over c subscript two, C subscript p equals C subscript one plus C subscript two for capacitors. Applying these formulas to the circuit consisting of two resistors in series and two capacitors in parallel gives R sub s equals R sub one plus R subscript two equals 10 ohm plus 10 ohm equals 20 ohm and C subscript p equals C subscript one plus C subscript two equals 20 p F plus 20 p F equals 40 p F. The time constant is tau equals RC equals open parenthesis 20 ohm close parenthesis open parenthesis 40 pF close parenthesis equals 800 p s.
, Cp = C1 + C2 for capacitors. Applying these formulas to the circuit consisting of two resistors in series and two capacitors in parallel gives Rs = R1 + R2 = 10 Ω + 10 Ω = 20 Ω and Cp = C1 + C2 = 20 pF + 20 pF = 40 pF. The time constant is τ = RC = (20 Ω) (40 pF) = 800 ps.
Correct Response: C. (Objective 0010) The time constant for a circuit consisting of capacitors and resistors is the product of the equivalent resistance and capacitance of the circuit. Answering the question requires determining the equivalent resistance and capacitance of each of the circuits. Analyzing each circuit requires using the formulas for two resistors and capacitors in series and parallel: R subscript s equals R sub one plus R subscript two, one over r subscript p equals one over r subscript one baseline plus one over r subscript two for resistors and one over c subscript s equals one over c subscript one baseline plus one over c subscript two, C subscript p equals C subscript one plus C subscript two for capacitors. Applying these formulas to the circuit consisting of two resistors in series and two capacitors in parallel gives R sub s equals R sub one plus R subscript two equals 10 ohm plus 10 ohm equals 20 ohm and C subscript p equals C subscript one plus C subscript two equals 20 p F plus 20 p F equals 40 p F. The time constant is tau equals RC equals open parenthesis 20 ohm close parenthesis open parenthesis 40 pF close parenthesis equals 800 p s.
Question 5
5. A circuit consists of a 9.0 V battery, a switch, a 1.0 MΩmega ohm resistor, and a 4.7 μFmicro farad capacitor connected in series. The voltage across the capacitor is initially 0.0 V. The switch is closed at t = 0.0 s. What is the voltage across the capacitor at t = 6.0 seconds?
- 2.5 V
- 6.5 V
- 7.1 V
- 8.7 V
Answer to question 5
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0010) When the switch is open there is no current flowing in the circuit and the voltages across the resistor and capacitor are zero. At the instant the switch is closed, charge begins to flow from the battery, VS, onto the negative plate and off of the positive plate of the capacitor C through the resistor R. The change in voltage across the plates of the capacitor follows the exponential form of VC = VS(1 − e–t/RC). In this circuit, the time constant, RC, is equal to (1.0 × 106 ohms)(4.7 × 10–6 farads) = 4.7 seconds. Solving for VC at t = 6.0 seconds gives: VC = 9(1 − e–6/4.7) = 9(1 − 0.28) = 6.5 V.
Correct Response: B. (Objective 0010) When the switch is open there is no current flowing in the circuit and the voltages across the resistor and capacitor are zero. At the instant the switch is closed, charge begins to flow from the battery, V subscript S, onto the negative plate and off of the positive plate of the capacitor C through the resistor R. The change in voltage across the plates of the capacitor follows the exponential form of V subscript C = V subscript S(1 minus e to the power of negative t over RC). In this circuit, the time constant, RC, is equal to (1.0 times 10 to the power of 6 ohms)(4.7 times 10 to the power of negative 6 farads) = 4.7 seconds. Solving for V subscript C at t = 6.0 seconds gives: V subscript C = 9(1 minus e to the power of negative 6 over 4.7) = 9(1 minus 0.28) = 6.5 V.
Question 6
6. Use the diagram below to answer the question that follows.
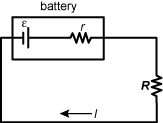
A small resistance little r is in series with the ideal voltage source Ɛ. There is a rectangle around these two components indicating that they make up a system. These two components are in series with a resistor indicated by a capital R. A current indicated by I flows from the ideal voltage source Ɛ through the two resistors. An arrow indicates that the currents starts at Ɛ and passes through the two resistors.
A battery with an ideal voltage of εepsilon providing current through an internal resistance r is used to model a constant current source. Which of the following describes the relationship between the internal resistance value, r, and the load resistance value R to satisfy the requirement of approximating a constant value of current flow, I, over a range of load resistances?
- r = Rr = upper R
- r ≪ Rr is much less than upper R
- r ≫ Rr is much greater than upper R
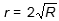 r = 2 square root upper R
r = 2 square root upper R
Answer to question 6
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0010) Applying Kirchhoff's voltage law to the circuit gives the current, I, described by the relationship: I = ε/(r + R). Assuming ε is a constant, I will remain essentially constant if the denominator (r + R) remains essentially constant. If R is allowed to change over a wide range of values, this condition will hold when r ≫ R.
Correct Response: C. (Objective 0010) Applying Kirchhoff's voltage law to the circuit gives the current, I, described by the relationship: I = epsilon over the quantity r + upper R. Assuming epsilon is a constant, I will remain essentially constant if the denominator (r + R) remains essentially constant. If R is allowed to change over a wide range of values, this condition will hold when r is much greater than R.
Question 7
7. A very large plane surface carries a uniform surface charge density of σ sigma . A cylinder of height h and radius r is placed on the plane such that the sides of the cylinder are perpendicular to the plane and the top and bottom of the cylinder are parallel to the plane, as shown in the diagram below.
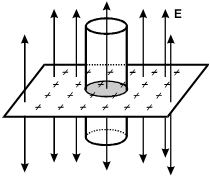
What is the magnitude of the electric field, E, through the cylinder above the plane?
Several electric field vectors are drawn perpendicular to the surface. Some of the vectors point upwards from the top of the plane, and other field vectors point downwards from the bottom side of the plane. The plane intersects a right circular cylinder. The sides of the cylinder are perpendicular to the plane. The top and bottom of the cylinder are parallel to the plane. The intersection of the plane and the cylinder is shaded. One electric field vector passes through the top of the cylinder, and one passes through the bottom of the cylinder.
- E =
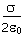 sigma over two times epsilon zero.
sigma over two times epsilon zero.
- E =
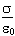 sigma over epsilon zero.
sigma over epsilon zero.
- E =
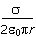 sigma over the product of two, epsilon zero, pi, and r.
sigma over the product of two, epsilon zero, pi, and r.
- E =
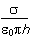 sigma over the product of epsilon zero, pi, and h.
sigma over the product of epsilon zero, pi, and h.
Answer to question 7
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0011) Gauss's law states
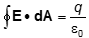 where q is how much charge is enclosed by the Gaussian surface in the integral. Since the plane is very large, we can model it by an infinite plane. By symmetry the electric field must point either directly away from or directly toward the plane. For a positive charge density the electric field must point away from the plane since lines of the E field begin on positive charges and terminate on negative charges. By symmetry the size of the electric field must be the same on one side of the plane a distance h/2 away as on the other side of the plane also a distance h/2 away. The dot product of the E with dA vectors for the curved surface of the cylinder is zero because E and dA are perpendicular on that surface. For the two surfaces parallel to the plane, E and dA are parallel to each other. Since the magnitude of the electric field is constant on these surfaces, each of these parallel surfaces contributes Eπr2 to the integral. The enclosed charge is σπr2. Putting these results into Guass's law gives ε02Eπr2 = σπr2. Solving gives E = σ/2ε0.
Correct Response: A. (Objective 0011) Gauss's law states the closed integral of E dot d upper A equals q over epsilon not where q is how much charge is enclosed by the Gaussian surface in the integral. Since the plane is very large, we can model it by an infinite plane. By symmetry the electric field must point either directly away from or directly toward the plane. For a positive charge density the electric field must point away from the plane since lines of the E field begin on positive charges and terminate on negative charges. By symmetry the size of the electric field must be the same on one side of the plane a distance h over 2 away as on the other side of the plane also a distance h/2 away. The dot product of the E with d A vectors for the curved surface of the cylinder is zero because E and d A are perpendicular on that surface. For the two surfaces parallel to the plane, E and d A are parallel to each other. Since the magnitude of the electric field is constant on these surfaces, each of these parallel surfaces contributes E pi r squared to the integral. The enclosed charge is sigma pi r squared. Putting these results into Guass's law gives epsilon not times 2 E pi r squared = sigma pi r squared. Solving gives E = sigma over 2 epsilon not.
where q is how much charge is enclosed by the Gaussian surface in the integral. Since the plane is very large, we can model it by an infinite plane. By symmetry the electric field must point either directly away from or directly toward the plane. For a positive charge density the electric field must point away from the plane since lines of the E field begin on positive charges and terminate on negative charges. By symmetry the size of the electric field must be the same on one side of the plane a distance h/2 away as on the other side of the plane also a distance h/2 away. The dot product of the E with dA vectors for the curved surface of the cylinder is zero because E and dA are perpendicular on that surface. For the two surfaces parallel to the plane, E and dA are parallel to each other. Since the magnitude of the electric field is constant on these surfaces, each of these parallel surfaces contributes Eπr2 to the integral. The enclosed charge is σπr2. Putting these results into Guass's law gives ε02Eπr2 = σπr2. Solving gives E = σ/2ε0.
Correct Response: A. (Objective 0011) Gauss's law states the closed integral of E dot d upper A equals q over epsilon not where q is how much charge is enclosed by the Gaussian surface in the integral. Since the plane is very large, we can model it by an infinite plane. By symmetry the electric field must point either directly away from or directly toward the plane. For a positive charge density the electric field must point away from the plane since lines of the E field begin on positive charges and terminate on negative charges. By symmetry the size of the electric field must be the same on one side of the plane a distance h over 2 away as on the other side of the plane also a distance h/2 away. The dot product of the E with d A vectors for the curved surface of the cylinder is zero because E and d A are perpendicular on that surface. For the two surfaces parallel to the plane, E and d A are parallel to each other. Since the magnitude of the electric field is constant on these surfaces, each of these parallel surfaces contributes E pi r squared to the integral. The enclosed charge is sigma pi r squared. Putting these results into Guass's law gives epsilon not times 2 E pi r squared = sigma pi r squared. Solving gives E = sigma over 2 epsilon not.
Question 8
8. A particle with positive charge q and speed v0 in the horizontal direction enters a region between the parallel plates of a capacitor. The distance between the plates is d and the voltage across the plates is V. In addition to a uniform electric field, there is a uniform magnetic field of magnitude B between the plates into the page as shown below.
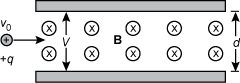
Between the two plates field lines of magnitude B are shown moving into the plane of the page. The positive particle labeled with v subscript zero and positive q travels into the field from the left moving to the right .
If the net Lorentz force on the particle is zero, what is the speed of the particle?
-
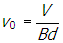 v subscript zero equals start fraction numerator v denominator b d
v subscript zero equals start fraction numerator v denominator b d
-
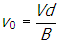 v subscript zero equals start fraction numerator v d denominator b
v subscript zero equals start fraction numerator v d denominator b
-
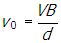 v subscript zero equals start fraction numerator v b denominator d
v subscript zero equals start fraction numerator v b denominator d
-
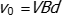 v subscript zero equals v b d
v subscript zero equals v b d
Answer to question 8
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0011) The Lorentz force describes the force on a point charge in an electromagnetic field and is given by F = q(E + v0 × B). It is given that the voltage between the plates is V and the electric field is uniform. Since the voltage is the work per unit charge, then V = Ed and the magnitude of the electric field is
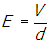 . The magnetic field is F = qv0 × B, where B and v0 are perpendicular. Because B is into the page, application of the right-hand rule shows that the magnetic force on the particle points from the bottom plate to the top plate of the capacitor. Since the net force on the particle is zero, the electric field must point from the top plate to the bottom plate of the capacitor and the magnitude of the electric force must equal the magnitude of the magnetic force. The magnitude of the magnetic force is FB = qv0B and the magnitude of the electric force is
. The magnetic field is F = qv0 × B, where B and v0 are perpendicular. Because B is into the page, application of the right-hand rule shows that the magnetic force on the particle points from the bottom plate to the top plate of the capacitor. Since the net force on the particle is zero, the electric field must point from the top plate to the bottom plate of the capacitor and the magnitude of the electric force must equal the magnitude of the magnetic force. The magnitude of the magnetic force is FB = qv0B and the magnitude of the electric force is
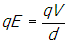 . Setting these two forces equal
. Setting these two forces equal
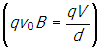 and cancelling and solving for v0 gives the result of
and cancelling and solving for v0 gives the result of
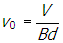 .
Correct Response: A. (Objective 0011) The Lorentz force describes the force on a point charge in an electromagnetic field and is given by F equals q open parenthesis E plus v subscript zero times B close parenthesis. It is given that the voltage between the plates is V and the electric field is uniform. Since the voltage is the work per unit charge, then V equals E d and the magnitude of the electric field is e equals v over d. The magnetic field is F equals q v sub zero times B, where B and v sub zero are perpendicular. Because B is into the page, application of the right-hand rule shows that the magnetic force on the particle points from the bottom plate to the top plate of the capacitor. Since the net force on the particle is zero, the electric field must point from the top plate to the bottom plate of the capacitor and the magnitude of the electric force must equal the magnitude of the magnetic force. The magnitude of the magnetic force is F B equals q v sub zero baseline B and the magnitude of the electric force is q e equals start fraction numerator q v denominator d end fraction. Setting these two forces equal open parenthesis q v sub zero baseline b equals start fraction numerator q v denominator d end fraction and cancelling and solving for v sub zero gives the result of v sub zero equals start fraction numerator v denominator b d end fraction.
.
Correct Response: A. (Objective 0011) The Lorentz force describes the force on a point charge in an electromagnetic field and is given by F equals q open parenthesis E plus v subscript zero times B close parenthesis. It is given that the voltage between the plates is V and the electric field is uniform. Since the voltage is the work per unit charge, then V equals E d and the magnitude of the electric field is e equals v over d. The magnetic field is F equals q v sub zero times B, where B and v sub zero are perpendicular. Because B is into the page, application of the right-hand rule shows that the magnetic force on the particle points from the bottom plate to the top plate of the capacitor. Since the net force on the particle is zero, the electric field must point from the top plate to the bottom plate of the capacitor and the magnitude of the electric force must equal the magnitude of the magnetic force. The magnitude of the magnetic force is F B equals q v sub zero baseline B and the magnitude of the electric force is q e equals start fraction numerator q v denominator d end fraction. Setting these two forces equal open parenthesis q v sub zero baseline b equals start fraction numerator q v denominator d end fraction and cancelling and solving for v sub zero gives the result of v sub zero equals start fraction numerator v denominator b d end fraction.
Question 9
9. Three identical point charges of magnitude q are located on the vertices of a right triangle with the dimensions shown below.
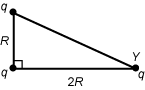
All vertices are labeled q. The horizontal base or leg is labeled two R and the vertical leg is labeled R. The vertex that is created with the hypotenuse and the long leg that is two R is additionally labeled Y.
What is the magnitude of the horizontal component of the force on the charge located at vertex Y?
-
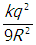 start fraction numerator k q squared denominator nine r squared end fraction
start fraction numerator k q squared denominator nine r squared end fraction
-
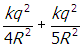 start fraction numerator k q squared denominator four r squared end fraction plus start fraction numerator k q squared denominator five r squared end fraction
start fraction numerator k q squared denominator four r squared end fraction plus start fraction numerator k q squared denominator five r squared end fraction
-
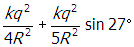 start fraction numerator k q squared denominator four r squared end fraction plus start fraction numerator k q squared denominator five r squared end fraction sine twenty seven degrees
start fraction numerator k q squared denominator four r squared end fraction plus start fraction numerator k q squared denominator five r squared end fraction sine twenty seven degrees
-
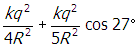 start fraction numerator k q squared denominator four r squared end fraction plus start fraction numerator k q squared denominator five r squared end fraction cosine twenty seven degrees
start fraction numerator k q squared denominator four r squared end fraction plus start fraction numerator k q squared denominator five r squared end fraction cosine twenty seven degrees
Answer to question 9
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0011) To find the horizontal component of the force on the charge located at vertex Y, find the sum of the horizontal components of the forces on the charge from the two other charges. From Coulomb's law, the magnitude of the force on the charge at Y from the top charge is
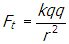 , where r is the hypotenuse of the triangle so that
, where r is the hypotenuse of the triangle so that
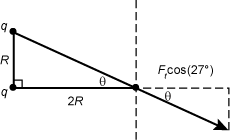
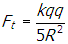 . The direction of the force vector is along the line shown in the diagram below.
. The direction of the force vector is along the line shown in the diagram below.
Notice that
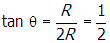 , so θ = 27°. The horizontal component from this force is thus
, so θ = 27°. The horizontal component from this force is thus
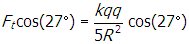 . The force from the bottom charge points in the horizontal direction and has magnitude
. The force from the bottom charge points in the horizontal direction and has magnitude
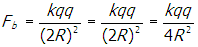 . The magnitude of the horizontal component of the force on the charge located at Y is the sum of these two quantities:
. The magnitude of the horizontal component of the force on the charge located at Y is the sum of these two quantities:
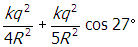 .
Correct Response: D. (Objective 0011) To find the horizontal component of the force on the charge located at vertex Y, find the sum of the horizontal components of the forces on the charge from the two other charges. From Coulomb's law, the magnitude of the force on the charge at Y from the top charge is f subscript t equals start fraction numerator k q q denominator r squared end fraction, where r is the hypotenuse of the triangle so that f subscript t equals start fraction numerator k q q denominator five r squared end fraction. The direction of the force vector is along the line shown in the following diagram. Right triangle. All vertices are labeled q. The horizontal base or leg is labeled two R and the vertical leg is labeled R. The vertex that is created with the hypotenuse and the long leg that is two R is additionally labeled Y and the angle of the triangle is labeled theta. At point y there is a dash vertical line and a dash horizontal line drawn. the hypotenuse of the triangle is extended past y and the angle created by this extended line and the horizontal dashed line is also labeled theta and f subscript t baseline cosine of twenty seven degrees. Notice that tangent of theta equals r over two r equals one half, so theta equals 27 degrees. The horizontal component from this force is thus f subscript t baseline cosine twenty seven degrees equals start fraction numerator k q q denominator five r squared cosine of twenty seven degrees. The force from the bottom charge points in the horizontal direction and has magnitude f subscript b equals start fraction numerator k q q denominator open parenthesis two r close parenthesis squared end fraction equals start fraction numerator k q q denominator open parenthesis two r close parenthesis squared equals start fraction numerator k q q denominator four r squared end fraction. The magnitude of the horizontal component of the force on the charge located at Y is the sum of these two quantities: start fraction numerator k q squared denominator four r squared end fraction plus start fraction numerator k q squared denominator five p square end fraction cosine twenty seven.
.
Correct Response: D. (Objective 0011) To find the horizontal component of the force on the charge located at vertex Y, find the sum of the horizontal components of the forces on the charge from the two other charges. From Coulomb's law, the magnitude of the force on the charge at Y from the top charge is f subscript t equals start fraction numerator k q q denominator r squared end fraction, where r is the hypotenuse of the triangle so that f subscript t equals start fraction numerator k q q denominator five r squared end fraction. The direction of the force vector is along the line shown in the following diagram. Right triangle. All vertices are labeled q. The horizontal base or leg is labeled two R and the vertical leg is labeled R. The vertex that is created with the hypotenuse and the long leg that is two R is additionally labeled Y and the angle of the triangle is labeled theta. At point y there is a dash vertical line and a dash horizontal line drawn. the hypotenuse of the triangle is extended past y and the angle created by this extended line and the horizontal dashed line is also labeled theta and f subscript t baseline cosine of twenty seven degrees. Notice that tangent of theta equals r over two r equals one half, so theta equals 27 degrees. The horizontal component from this force is thus f subscript t baseline cosine twenty seven degrees equals start fraction numerator k q q denominator five r squared cosine of twenty seven degrees. The force from the bottom charge points in the horizontal direction and has magnitude f subscript b equals start fraction numerator k q q denominator open parenthesis two r close parenthesis squared end fraction equals start fraction numerator k q q denominator open parenthesis two r close parenthesis squared equals start fraction numerator k q q denominator four r squared end fraction. The magnitude of the horizontal component of the force on the charge located at Y is the sum of these two quantities: start fraction numerator k q squared denominator four r squared end fraction plus start fraction numerator k q squared denominator five p square end fraction cosine twenty seven.
Question 10
10. The diagram below shows an air core toroid consisting of a wire carrying current I coiled with N loops bent in a circle of radius R.
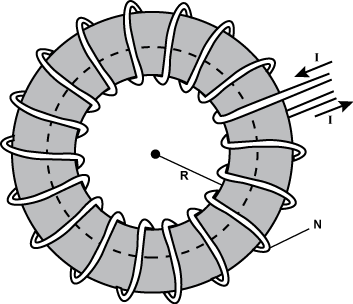
there is a wire labeled i that is coiled around the donut with n number of loops coming onto the donut like object and coming off the object
Assuming that the magnetic field, B, is constant in magnitude along and tangent to the dashed circular path inside the toroid, which of the following equations could be used to find the magnetic field?
- 2πrB = μ0 subscript 0 NI
- 2πr = μ0 subscript 0 NIB
- πr2B = μ0 subscript 0 NI
- πr2 = μ0 subscript 0 NIB
Answer to question 10
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0011) The object shown is a toroid, a doughnut-shaped object with wire coiled around its exterior. Current in the wire produces a magnetic field. Assuming that the field is constant along and tangent to the circular curve, Ampere's law can be applied to the dotted circular curve inside the toroid. Ampere's law states that
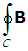 • dℓ = μ0Ienclosed, where B is the magnetic field,
• dℓ = μ0Ienclosed, where B is the magnetic field,
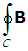 • dℓ is the line integral around the closed path C, μ0 is the magnetic permeability of free space, and Ienclosed is equal to the total current enclosed by the curve C. Since the field is constant and tangent to the curve, B • dℓ = Bdℓ, and the line integral is just the product of the magnitude of the field B and 2πr, the length of the curve. The line integral is equal to μ0 times the current enclosed by the curve, which can be defined by the current passing through any open surface connecting C. If the surface is taken to be a disk centered at O with circumference given by the dotted circular curve, then the enclosed current is the number of current loops, N, times the current in each loop, I. Therefore, Ampere's law gives
• dℓ is the line integral around the closed path C, μ0 is the magnetic permeability of free space, and Ienclosed is equal to the total current enclosed by the curve C. Since the field is constant and tangent to the curve, B • dℓ = Bdℓ, and the line integral is just the product of the magnitude of the field B and 2πr, the length of the curve. The line integral is equal to μ0 times the current enclosed by the curve, which can be defined by the current passing through any open surface connecting C. If the surface is taken to be a disk centered at O with circumference given by the dotted circular curve, then the enclosed current is the number of current loops, N, times the current in each loop, I. Therefore, Ampere's law gives
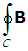 • dℓ = μ0Ienclosed = 2πrB = μ 0NI.
Correct Response: A. (Objective 0011) The object shown is a toroid, a doughnut-shaped object with wire coiled around its exterior. Current in the wire produces a magnetic field. Assuming that the field is constant along and tangent to the circular curve, Ampere's law can be applied to the dotted circular curve inside the toroid. Ampere's law states that closed line integral around the closed curve c of upper bold b dot d bold l equals mu subscript 0 baseline I subscript enclosed, where B is the magnetic field, closed line integral around the closed curve c of upper bold b dot d l is the line integral around the closed path C, mu subscript 0 is the magnetic permeability of free space, and I subscript enclosed is equal to the total current enclosed by the curve C. Since the field is constant and tangent to the curve, B dot d l equals B d l, and the line integral is just the product of the magnitude of the field B and 2 pi r, the length of the curve. The line integral is equal to mu subscript 0 times the current enclosed by the curve, which can be defined by the current passing through any open surface connecting C. If the surface is taken to be a disk centered at O with circumference given by the dotted circular curve, then the enclosed current is the number of current loops, N, times the current in each loop, I. Therefore, Ampere's law gives closed line integral around the closed curve c of upper bold b dot d l equals mu subscript 0 baseline I sub enclosed equals 2 pi r B equals mu subscript 0 baseline N I.
• dℓ = μ0Ienclosed = 2πrB = μ 0NI.
Correct Response: A. (Objective 0011) The object shown is a toroid, a doughnut-shaped object with wire coiled around its exterior. Current in the wire produces a magnetic field. Assuming that the field is constant along and tangent to the circular curve, Ampere's law can be applied to the dotted circular curve inside the toroid. Ampere's law states that closed line integral around the closed curve c of upper bold b dot d bold l equals mu subscript 0 baseline I subscript enclosed, where B is the magnetic field, closed line integral around the closed curve c of upper bold b dot d l is the line integral around the closed path C, mu subscript 0 is the magnetic permeability of free space, and I subscript enclosed is equal to the total current enclosed by the curve C. Since the field is constant and tangent to the curve, B dot d l equals B d l, and the line integral is just the product of the magnitude of the field B and 2 pi r, the length of the curve. The line integral is equal to mu subscript 0 times the current enclosed by the curve, which can be defined by the current passing through any open surface connecting C. If the surface is taken to be a disk centered at O with circumference given by the dotted circular curve, then the enclosed current is the number of current loops, N, times the current in each loop, I. Therefore, Ampere's law gives closed line integral around the closed curve c of upper bold b dot d l equals mu subscript 0 baseline I sub enclosed equals 2 pi r B equals mu subscript 0 baseline N I.
Question 11
11. The specifications for a DC electric motor provide data for both the start-up current and the current required to operate at full mechanical load. This information shows that the current required by the motor when power is initially applied can be many times greater than when the motor is running at full speed. Which of the following fundamental laws related to electromagnetism provides an explanation for this phenomenon?
- Kirchhoff's current law
- Ampere's law
- Ohm's law
- Lenz's law
Answer to question 11
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0011) The instant that power is supplied to the electric motor, the initial opposition to current flow in the stationary armature of the electric motor is caused by the resistance of the coil windings. This is a relatively a low resistance. Hence, the initial current is relatively large. The current creates a magnetic field in the armature coil which interacts with the magnetic field of the permanent magnet, producing a torque on the armature shaft and causing rotation. Rotation of the armature coil relative to the magnetic field produces an induced voltage, typically referred to as “back EMF,” in this coil which is in opposition to the applied voltage. The induced voltage, in opposition to the applied voltage, reduces the current flow through the armature. This effect is described by Lenz's law, which states that the direction of current induced in a conductor by a changing magnetic field will create a magnetic field, and thus an induced voltage, that opposes the change that produced it. The total opposition to current flow in the armature of a motor operating under load is limited by both the coil's resistance and the effect of the back EMF, eventually resulting in an equilibrium speed.
Correct Response: D. (Objective 0011) The instant that power is supplied to the electric motor, the initial opposition to current flow in the stationary armature of the electric motor is caused by the resistance of the coil windings. This is a relatively a low resistance. Hence, the initial current is relatively large. The current creates a magnetic field in the armature coil which interacts with the magnetic field of the permanent magnet, producing a torque on the armature shaft and causing rotation. Rotation of the armature coil relative to the magnetic field produces an induced voltage, typically referred to as “back EMF,” in this coil which is in opposition to the applied voltage. The induced voltage, in opposition to the applied voltage, reduces the current flow through the armature. This effect is described by Lenz's law, which states that the direction of current induced in a conductor by a changing magnetic field will create a magnetic field, and thus an induced voltage, that opposes the change that produced it. The total opposition to current flow in the armature of a motor operating under load is limited by both the coil's resistance and the effect of the back EMF, eventually resulting in an equilibrium speed.
Question 12
12. Which of the following provides an explanation of why the unit for electric potential difference, the volt, is equivalent in metric base units to (N•m2/s2)/C(units of newton-meter squared per second squared) per coulomb?
- The definition of potential difference, measured in volts, is the work done per unit charge in moving a test charge through some distance in an electric field.
- The potential difference between two points in an electric field is equal to the ratio of the force on a charge to the amount of charge.
- The volt is proportional to the power, and inversely proportional to the charge required to maintain equilibrium of a charged object in an electric field.
- The potential difference in an electric field is equal to the energy change per unit change that exists along a line of equipotential.
Answer to question 12
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0011) The potential difference between two points in an electric field is described by the change in potential energy, ΔU per charge,
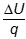 . This change in energy is related to the work done on the charge, W = F • d, where the force required to move the charge is the product of the amount of charge, q, and E, the electric field. Since F = qE, combining this information for a unit analysis gives
. This change in energy is related to the work done on the charge, W = F • d, where the force required to move the charge is the product of the amount of charge, q, and E, the electric field. Since F = qE, combining this information for a unit analysis gives 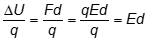 which has units of (N•m/s2)(m)/C or (N•m2/s2)/C.
Correct Response: A. (Objective 0011) The potential difference between two points in an electric field is described by the change in potential energy, delta U per charge, delta U over q. This change in energy is related to the work done on the charge, W equals F dot d, where the force required to move the charge is the product of the amount of charge, q, and E, the electric field. Since F equals q E, combining this information for a unit analysis gives delta U over q equals F d over q equals qEd over q equals Ed which has units of newton meter per second squared times meters all over coulomb or newton meter squared per second squared per coulomb.
which has units of (N•m/s2)(m)/C or (N•m2/s2)/C.
Correct Response: A. (Objective 0011) The potential difference between two points in an electric field is described by the change in potential energy, delta U per charge, delta U over q. This change in energy is related to the work done on the charge, W equals F dot d, where the force required to move the charge is the product of the amount of charge, q, and E, the electric field. Since F equals q E, combining this information for a unit analysis gives delta U over q equals F d over q equals qEd over q equals Ed which has units of newton meter per second squared times meters all over coulomb or newton meter squared per second squared per coulomb.
Question 13
13. A square wire loop of side length x is rotated in a constant magnetic field at an angular speed ω, as indicated in the diagram below.
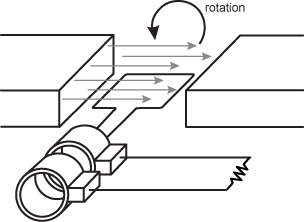
The square wire loop is in the field lines and shown rotating counterclockwise. The wire loop is connected to a voltmeter with a resistor attached, both of which are outside of the magnetic field.
As the loop rotates, a voltmeter reads a root-mean-square (RMS) value of 80 V across the resistor. If the side of the loop is changed to
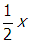 one half x
and the rotational speed of the loop is changed to
one half x
and the rotational speed of the loop is changed to
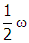 one half omega, what RMS value will the voltmeter measure?
one half omega, what RMS value will the voltmeter measure?
- 10 V
- 20 V
- 40 V
- 80 V
Answer to question 13
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0012) As the wire coil rotates, the magnetic field through the coil changes, and by Faraday's law an emf is created in the loop. The voltmeter reads this emf. Faraday's law states that the emf depends on the rate of change of flux through the surface of the coil. The flux is
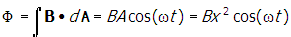 , where B is the magnetic field, A = x2 is the area of the loop, and θ = ωt is the angle between the vector normal to the surface of the loop and B. Using Faraday's law to get the emf, ε , gives
, where B is the magnetic field, A = x2 is the area of the loop, and θ = ωt is the angle between the vector normal to the surface of the loop and B. Using Faraday's law to get the emf, ε , gives
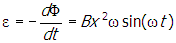 . Reducing a side of the square loop to
. Reducing a side of the square loop to
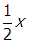 reduces the area to
reduces the area to
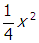 , so the maximum flux and the maximum emf will be reduced to
, so the maximum flux and the maximum emf will be reduced to
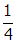 of their previous values from this factor. Slowing the rotational speed, ω , to half its initial value will reduce the maximum emf by another factor of
of their previous values from this factor. Slowing the rotational speed, ω , to half its initial value will reduce the maximum emf by another factor of
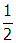 . Therefore, the maximum emf will be reduced by a factor of
. Therefore, the maximum emf will be reduced by a factor of
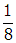 . The voltmeter reads the RMS value of the emf, which is just proportional to the maximum emf value. Since the initial voltmeter reading is 80 V, the voltmeter will read 10 V under the new conditions.
Correct Response: A. (Objective 0012) As the wire coil rotates, the magnetic field through the coil changes, and by Faraday's law an emf is created in the loop. The voltmeter reads this emf. Faraday's law states that the emf depends on the rate of change of flux through the surface of the coil. The flux is phi equals integral bold upper b dot d upper bold a equals upper b upper a cosine of open parenthesis omega t close parenthesis equals upper b x squared cosine of open parenthesis omega t close parenthesis where B is the magnetic field, A equals x squared is the area of the loop, and theta equals omega t is the angle between the vector normal to the surface of the loop and B. Using Faraday's law to get the emf, epsilon, gives epsilon equals negative start fraction numerator d phi denominator d t end fraction equals upper b x squared omega sine of open parenthesis omega t close parenthesis. Reducing a side of the square loop to one half x reduces the area to one fourth x squared, so the maximum flux and the maximum emf will be reduced to one fourth of their previous values from this factor. Slowing the rotational speed, omega, to half its initial value will reduce the maximum emf by another factor of one half. Therefore, the maximum emf will be reduced by a factor of one eighth. The voltmeter reads the R M S value of the emf, which is just proportional to the maximum emf value. Since the initial voltmeter reading is 80 V, the voltmeter will read 10 V under the new conditions.
. The voltmeter reads the RMS value of the emf, which is just proportional to the maximum emf value. Since the initial voltmeter reading is 80 V, the voltmeter will read 10 V under the new conditions.
Correct Response: A. (Objective 0012) As the wire coil rotates, the magnetic field through the coil changes, and by Faraday's law an emf is created in the loop. The voltmeter reads this emf. Faraday's law states that the emf depends on the rate of change of flux through the surface of the coil. The flux is phi equals integral bold upper b dot d upper bold a equals upper b upper a cosine of open parenthesis omega t close parenthesis equals upper b x squared cosine of open parenthesis omega t close parenthesis where B is the magnetic field, A equals x squared is the area of the loop, and theta equals omega t is the angle between the vector normal to the surface of the loop and B. Using Faraday's law to get the emf, epsilon, gives epsilon equals negative start fraction numerator d phi denominator d t end fraction equals upper b x squared omega sine of open parenthesis omega t close parenthesis. Reducing a side of the square loop to one half x reduces the area to one fourth x squared, so the maximum flux and the maximum emf will be reduced to one fourth of their previous values from this factor. Slowing the rotational speed, omega, to half its initial value will reduce the maximum emf by another factor of one half. Therefore, the maximum emf will be reduced by a factor of one eighth. The voltmeter reads the R M S value of the emf, which is just proportional to the maximum emf value. Since the initial voltmeter reading is 80 V, the voltmeter will read 10 V under the new conditions.
Question 14
14. The diagram below shows a bar magnet of unknown polarity and a wire coil attached to a resistor.
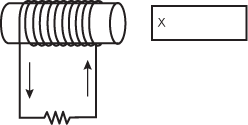
The current flow is shown as traveling counterclockwise righthand side of the cylinder. The magnet is shown with one pole marked X facing the right hand side of the cylinder.
In which of the following cases will positive current have the direction shown?
- X is a north pole and the magnet is stationary.
- X is a south pole and the magnet is stationary.
- X is a north pole moving toward the coil.
- X is a south pole moving toward the coil.
Answer to question 14
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0012) By Faraday's law, since there is a current in the coil and no external emf, the current is produced by a changing magnetic field, so the bar magnet must be in motion. From the right-hand rule, curling the fingers of the right hand in the direction of the induced current shows that the north pole of the induced field in the coil points to the right, and the south pole points to the left. Lenz's law states that when a changing magnetic field produces an emf, the polarity of the emf is produced to oppose that change in magnetic flux. The induced emf produces the current in the direction shown. Therefore, the north pole in the coil is produced to oppose the change in flux. In this case, the north pole of the magnetic field in the coil is produced to repel the pole of the bar magnet. Since like poles repel, X must be a north pole, and since the magnet is in motion as described above, X must be a north pole moving toward the coil to induce the current in the direction shown.
Correct Response: C. (Objective 0012) By Faraday's law, since there is a current in the coil and no external emf, the current is produced by a changing magnetic field, so the bar magnet must be in motion. From the right-hand rule, curling the fingers of the right hand in the direction of the induced current shows that the north pole of the induced field in the coil points to the right, and the south pole points to the left. Lenz's law states that when a changing magnetic field produces an emf, the polarity of the emf is produced to oppose that change in magnetic flux. The induced emf produces the current in the direction shown. Therefore, the north pole in the coil is produced to oppose the change in flux. In this case, the north pole of the magnetic field in the coil is produced to repel the pole of the bar magnet. Since like poles repel, X must be a north pole, and since the magnet is in motion as described above, X must be a north pole moving toward the coil to induce the current in the direction shown.
Question 15
15. Which of the following situations will produce an electromagnetic wave?
- an electric dipole
- an oscillating charge
- a constant current in a wire
- a nonuniform charge distribution
Answer to question 15
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0012) According to Maxwell's equations, electromagnetic waves are oscillating electric and magnetic fields. A changing electric field produces a changing magnetic field which produces a changing electric field and so on. Once electromagnetic waves are produced, they are perpetuated by the regenerative relationship between changing electric fields and changing magnetic fields. These changing fields propagate through a vacuum at the speed of light. An analysis of Maxwell's equations shows that these waves are generated when charges accelerate. Of the responses given, only the oscillating charge is undergoing acceleration.
Correct Response: B. (Objective 0012) According to Maxwell's equations, electromagnetic waves are oscillating electric and magnetic fields. A changing electric field produces a changing magnetic field which produces a changing electric field and so on. Once electromagnetic waves are produced, they are perpetuated by the regenerative relationship between changing electric fields and changing magnetic fields. These changing fields propagate through a vacuum at the speed of light. An analysis of Maxwell's equations shows that these waves are generated when charges accelerate. Of the responses given, only the oscillating charge is undergoing acceleration.
Question 16
16. Which of the following is the best example of a process that will generate an electromagnetic wave?
- a current-carrying wire
- an oscillating electric dipole
- a uniform magnetic field
- a charged capacitor
Answer to question 16
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0012) An electromagnetic wave is energy that propagates through space as changing electric and magnetic fields. According to Maxwell's equations, which are a part of classical electrodynamics, electromagnetic waves are produced by accelerating charges. If an object is oscillating, it is accelerating. When a charge oscillates, it creates an oscillating electric field, which then creates an oscillating magnetic field, which creates an oscillating electric field, etc. These electric and magnetic fields propagate through a vacuum at the speed of light. The frequency of the wave is equal to the frequency of oscillation. An electric dipole consists of a positive and negative charge equal in magnitude. These two oscillating particles contribute to the electromagnetic wave.
Correct Response: B. (Objective 0012) An electromagnetic wave is energy that propagates through space as changing electric and magnetic fields. According to Maxwell's equations, which are a part of classical electrodynamics, electromagnetic waves are produced by accelerating charges. If an object is oscillating, it is accelerating. When a charge oscillates, it creates an oscillating electric field, which then creates an oscillating magnetic field, which creates an oscillating electric field, etc. These electric and magnetic fields propagate through a vacuum at the speed of light. The frequency of the wave is equal to the frequency of oscillation. An electric dipole consists of a positive and negative charge equal in magnitude. These two oscillating particles contribute to the electromagnetic wave.
Question 17
17. A person would like to use a thin converging lens to generate a real image of an object placed 20 cm in front of the lens. The height of the object is 3.0 cm, and desired height of the image is 6.0 cm. What focal length should the lens have?
- 6.7 cm
- 9.0 cm
- 13.3 cm
- 40 cm
Answer to question 17
- Answer Enter to expand or collapse answer. Answer expanded
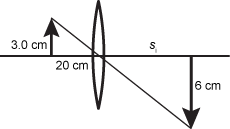
- Correct Response: C. (Objective 0013) The diagram below shows the principal ray going through the center of the converging lens.
The two triangles formed in this diagram are similar, so 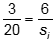 . Solving gives si equals 40 cm. Next we can use
. Solving gives si equals 40 cm. Next we can use 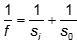 or
or 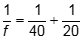 , and solving gives f = 13.3 cm.
Correct Response: C. (Objective 0013) The diagram below shows the principal ray going through the center of the converging lens.
, and solving gives f = 13.3 cm.
Correct Response: C. (Objective 0013) The diagram below shows the principal ray going through the center of the converging lens.
The diagram shows a thin lens. Marked at distance 20 cm to the left of the lens is an up right arrow labeled 3.0 cm in height. At a distance labeled s subscript i to the right of the lens is a downward arrow, below the optical axis, labeled 6 cm. A line connecting the tops of the two arrows is drawn. The line passes through the center of the lens at the optical axis. The two triangles are clearly similar.
The two triangles formed in this diagram are similar, so 3 over 20 equals 6 over s subscript i. Solving gives s subscript i equals 40 cm. Next we can use 1 over f equals 1 over s subscipt i plus 1 over s subscript o or 1 over f equals 1 over 40 plus 1 over 20, and solving gives f equals 13.3 cm.
Question 18
18. The diagram below shows a ray of light incident on a piece of glass. The index of refraction of air is n = 1.0, and that of the glass is n = 1.5. The angle between the incident and the reflected light ray is θ = 60° degrees .
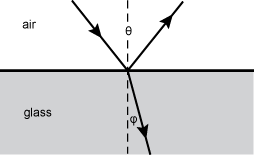
bottom portion is the glass and the top portion is air. the light hits the glass at a sixty degree angle and reflects off making a sixty degree angle labeled theta. There is a vertical dashed line intersecting the angle theta. below the glass the light ray continues in a negative fashion at a smaller angle phi off of the vertical line intersecting the larger angle at the top of the glass
Which of the following is closest to the measure of φphi?
- 15° degrees
- 17° degrees
- 19° degrees
- 35° degrees
Answer to question 18
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0013) When light travels from one medium to another, it changes speed, which causes the wave to bend. Using the ray model of light, the amount of bending, or refraction, is given by Snell's law, n1 sin θi = n2 sin θr, where n1 is the index of refraction of the optical medium of the incident light, n2 is the index of refraction of the refracted light, and θi and θr are the angles of incidence and refraction, respectively. The angle of incidence is the angle made with the line normal (perpendicular) to the surface in the initial medium and the angle of refraction is with respect to the normal in the second medium. In the diagram above, the normal is the vertical line. Therefore, the angle of incidence is
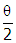 = 30° and the angle of refraction is φ . Using the values given and Snell's law, 1.0 sin 30° = 1.5 sin φ °, so sin φ = and sin−1 φ =
= 30° and the angle of refraction is φ . Using the values given and Snell's law, 1.0 sin 30° = 1.5 sin φ °, so sin φ = and sin−1 φ =
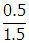 , or θ = 19.47 or 19°.
Correct Response: C. (Objective 0013) When light travels from one medium to another, it changes speed, which causes the wave to bend.
, or θ = 19.47 or 19°.
Correct Response: C. (Objective 0013) When light travels from one medium to another, it changes speed, which causes the wave to bend.
Using the ray model of light, the amount of bending, or refraction, is given by Snell's law, n subscript one sine theta sub i equals n sub two baseline sine theta subscript r, where n subscript one is the index of refraction of the optical medium of the incident light, n subscript two is the index of refraction of the refracted light, and theta subscript i and theta subscript r are the angles of incidence and refraction, respectively. The angle of incidence is the angle made with the line normal (perpendicular) to the surface in the initial medium and the angle of refraction is with respect to the normal in the second medium.
In the diagram above, the normal is the vertical line. Therefore, the angle of incidence is theta over two equals 30 degrees and the angle of refraction is phi. Using the values given and Snell's law, 1.0 sine 30 degrees equals 1.5 sine phi degrees, so sine phi equals and sine minus 1 phi equals zero point five over one point five, or theta equals 19.47 or 19 degrees.
Question 19
19. The ray diagram below shows the optics of an object on the optical axis of a concave mirror.
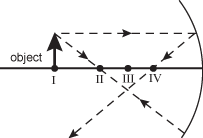
Four points labeled I, II, III, and IV are along the axis with I furthest from the mirror. At point I is an arrow normal to the axis labeled "object". A dashed ray is shown from the top of the arrow through point II at the axis and then reflecting from the mirror and back to the arrow. A second ray is shown from the arrow parallel to the axis to the mirror and reflected down through the axis at point IV. Point III is midway between points II and IV, at the same position on the axis where the two rays intersect below the axis.
Which of the following statements about this system is true?
- The mirror has a focal point at II and forms a virtual inverted image between I and II.
- The mirror has a focal point at II and forms a real upright image at IV.
- The mirror has a focal point at IV and forms a real inverted image at III.
- The mirror has a focal point between II and III and forms a virtual upright image at IV.
Answer to question 19
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0013) The focal point of a mirror is the point at which light rays parallel to the optical axis intersect the axis after being reflected from the mirror. According to the diagram, the focal point of the mirror is at point IV and light rays from the top of the object intersect beneath point III, forming an inverted image. This can be seen further by tracing a ray from the top of the object through point IV. The reflected ray will be parallel to the optical axis and intersect the other rays from the top of the image.
Correct Response: C. (Objective 0013) The focal point of a mirror is the point at which light rays parallel to the optical axis intersect the axis after being reflected from the mirror. According to the diagram, the focal point of the mirror is at point I V and light rays from the top of the object intersect beneath point III, forming an inverted image. This can be seen further by tracing a ray from the top of the object through point IV. The reflected ray will be parallel to the optical axis and intersect the other rays from the top of the image.
Question 20
20. An optical system consists of two converging lenses. The objective lens has a focal length of 1.0 cm and the eyepiece has a focal length of 4.0 cm. An object is located at a distance of 1.5 cm from the objective lens. The eyepiece is used as a magnifying glass.
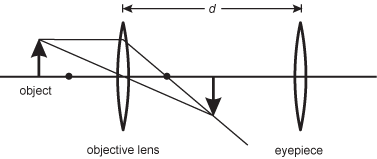
They are separated by a distance d and shown with an axis drawn through the center of the two. An upward object arrow is shown to the left of the objective with one ray shown from the tip of the object arrow passing through the axis at the center of the objective lens, and connecting to the tip of a downward inverted image. A second ray is shown from the tip or the object arrow parallel to the axis to the objective lens then turning to meet the tip of the inverted image below the axis.
Between which of the following distances from the objective lens can the eyepiece be placed so that a person looking through the eyepiece will see a virtual inverted image of the object?
- 0.0 cm and 1.0 cm
- 1.0 cm and 1.5 cm
- 3.0 cm and 7.0 cm
- 7.0 cm and 16 cm
Answer to question 20
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0013) In a system consisting of two lenses, the objective lens is used to form an image that is then used as the object of the second lens—in this case, the eyepiece. Since the object is at a distance greater than the focal length of the objective lens, the objective lens forms an inverted image of the object. The eyepiece is then used as a magnifying glass to create a virtual image of the inverted image. In order for a converging lens (the eyepiece) to create a virtual image of an object, the object must be located between the eyepiece and the focal point of the lens. Therefore, the eyepiece must be located between 0.0 cm and 4.0 cm from the inverted image formed by the objective lens. To find where the inverted image is located, apply the thin lens equation to the objective lens,
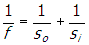 , where f is the focal length and so and si are the distances from the objective lens of the object and the image, respectively. Since f = 1.0 cm and so = 1.5 cm, the equation becomes
, where f is the focal length and so and si are the distances from the objective lens of the object and the image, respectively. Since f = 1.0 cm and so = 1.5 cm, the equation becomes
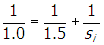 . Solving for si gives si = 3.0 cm, so the inverted image is formed 3.0 cm to the right of the objective lens. Since the eyepiece must be located between 0.0 cm and 4.0 cm from the inverted image to create a virtual image, the eyepiece must be located between 3.0 cm and 7.0 cm from the objective lens.
Correct Response: C. (Objective 0013) (Objective 0013) In a system consisting of two lenses, the objective lens is used to form an image that is then used as the object of the second lens—in this case, the eyepiece. Since the object is at a distance greater than the focal length of the objective lens, the objective lens forms an inverted image of the object. The eyepiece is then used as a magnifying glass to create a virtual image of the inverted image. In order for a converging lens (the eyepiece) to create a virtual image of an object, the object must be located between the eyepiece and the focal point of the lens. Therefore, the eyepiece must be located between 0.0 cm and 4.0 cm from the inverted image formed by the objective lens. To find where the inverted image is located, apply the thin lens equation to the objective lens, one over f equals one over s subscript zero baseline plus one over s subscript i, where f is the focal length and s subscript zero and s subscript i are the distances from the objective lens of the object and the image, respectively. Since f equals 1.0 cm and s subscript zero equals 1.5
cm, the equation becomes one over one point zero equals one over one point five plus one over s subscript i. Solving for s subscript i gives s subscript i equals 3.0 cm, so the inverted image is formed 3.0 cm to the right of the objective lens. Since the eyepiece must be located between 0.0 cm and 4.0 cm from the inverted image to create a virtual image, the eyepiece must be located between 3.0 cm and 7.0 cm from the objective lens.
. Solving for si gives si = 3.0 cm, so the inverted image is formed 3.0 cm to the right of the objective lens. Since the eyepiece must be located between 0.0 cm and 4.0 cm from the inverted image to create a virtual image, the eyepiece must be located between 3.0 cm and 7.0 cm from the objective lens.
Correct Response: C. (Objective 0013) (Objective 0013) In a system consisting of two lenses, the objective lens is used to form an image that is then used as the object of the second lens—in this case, the eyepiece. Since the object is at a distance greater than the focal length of the objective lens, the objective lens forms an inverted image of the object. The eyepiece is then used as a magnifying glass to create a virtual image of the inverted image. In order for a converging lens (the eyepiece) to create a virtual image of an object, the object must be located between the eyepiece and the focal point of the lens. Therefore, the eyepiece must be located between 0.0 cm and 4.0 cm from the inverted image formed by the objective lens. To find where the inverted image is located, apply the thin lens equation to the objective lens, one over f equals one over s subscript zero baseline plus one over s subscript i, where f is the focal length and s subscript zero and s subscript i are the distances from the objective lens of the object and the image, respectively. Since f equals 1.0 cm and s subscript zero equals 1.5
cm, the equation becomes one over one point zero equals one over one point five plus one over s subscript i. Solving for s subscript i gives s subscript i equals 3.0 cm, so the inverted image is formed 3.0 cm to the right of the objective lens. Since the eyepiece must be located between 0.0 cm and 4.0 cm from the inverted image to create a virtual image, the eyepiece must be located between 3.0 cm and 7.0 cm from the objective lens.
Question 21
21. Which of the following statements describes the separation of white light into spectral colors as it passes from air through a glass prism?
- Different path lengths corresponding to different wavelengths produce a multicolored interference pattern.
- Frequency modulation occurs as the light waves interact and scatter from the molecules in the material.
- Different wavelengths in the incident light are bent by different amounts as they pass through the material.
- The electric fields vectors of the incident wave are oriented in different directions, resulting in different refraction angles.
Answer to question 21
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0013) White light consists of a range of electromagnetic waves qualitatively described by the visible colors red through violet. These correspond to wavelengths ranging from longer to shorter with frequencies that are inversely proportional to the wavelengths. When light passes from air into a more dense medium, such as glass, absorption and re-emission of energy occurs at the atomic level. This effect is wavelength dependent with longer wavelengths (red) being slowed down more than shorter ones (violet). The index of refraction of a material, n, characterizes its tendency to slow down the passage of light through this process, resulting in the bending of light rays, or refraction. In glass, or other “clear” materials used for making prisms, the index of refraction varies a small amount for different wavelengths. This effectively separates different bands of wavelengths, corresponding to colors, as they pass through and emerge from the prism.
Correct Response: C. (Objective 0013) White light consists of a range of electromagnetic waves qualitatively described by the visible colors red through violet. These correspond to wavelengths ranging from longer to shorter with frequencies that are inversely proportional to the wavelengths. When light passes from air into a more dense medium, such as glass, absorption and re-emission of energy occurs at the atomic level. This effect is wavelength dependent with longer wavelengths (red) being slowed down more than shorter ones (violet). The index of refraction of a material, n, characterizes its tendency to slow down the passage of light through this process, resulting in the bending of light rays, or refraction. In glass, or other “clear” materials used for making prisms, the index of refraction varies a small amount for different wavelengths. This effectively separates different bands of wavelengths, corresponding to colors, as they pass through and emerge from the prism.
Question 22
22. Unpolarized light of intensity I is incident on a system of two polarizers. Two photometers are positioned as shown in the diagram below. The axis of the second polarizer is aligned at 60° degrees with respect to the vertical axis of the first polarizer.
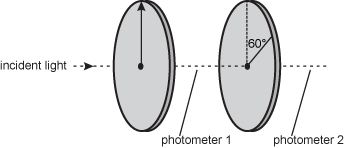
The second polarization in the second is rotated sixty degrees from the first. Photometer one is between the two polarizers, and Photometer two is reading after the light passes through both the polarizers.
What intensity will the two photometers register?
- Photometer 1 will read I and photometer 2 will read
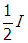 one half I.
one half I.
- Photometer 1 will read I and photometer 2 will read
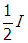 one half I.
one half I.
- Photometer 1 will read
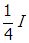 one fourth i
and photometer 2 will read
one fourth i
and photometer 2 will read
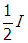 one half i.
one half i.
- Photometer 1 will read
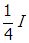 one fourth i
and photometer 2 will read
one fourth i
and photometer 2 will read
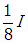 one eighth i.
one eighth i.
Answer to question 22
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0014) Electromagnetic waves consist of oscillating electric and magnetic fields that propagate through space at the speed of light, c. The waves are transverse: the fields oscillate in a direction perpendicular to the direction of wave propagation. Unpolarized light consists of a superposition of many light waves that have their electric and magnetic field vectors pointing in random directions perpendicular to the wave propagation. Since the magnitude of the magnetic field is small compared to the electric field, it is the electric field that interacts with matter most strongly. Polarizing filters are typically made of plastic that contains tiny crystals arranged in the same direction so that they transmit only the component of the electric field parallel to the direction of alignment; the perpendicular component of the electric field is absorbed. Each electric field vector can be resolved to a component that is parallel and a component that is perpendicular to the polarizing axis. The parallel component will pass through the filter and the perpendicular component will be absorbed. Since the electric field vectors are randomly aligned in unpolarized light, half of the light intensity corresponds to the electric field components parallel to the polarizing axis. Therefore, the photometer between the filters will read
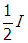 . Malus's law can be used to find the amount of light transmitted through the second filter. The intensity of transmitted light is It = I0 cos2 θ , where I0 is the intensity of the polarized beam between the two filters and θ is the angle between the two polarizing axes. Since θ = 60° and cos 60° =
. Malus's law can be used to find the amount of light transmitted through the second filter. The intensity of transmitted light is It = I0 cos2 θ , where I0 is the intensity of the polarized beam between the two filters and θ is the angle between the two polarizing axes. Since θ = 60° and cos 60° =
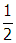 , cos2 θ =
, cos2 θ =
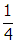 , and I0 =
, and I0 =
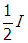 , the second photometer will register an intensity of
, the second photometer will register an intensity of
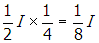 .
Correct Response: D. (Objective 0014) Electromagnetic waves consist of oscillating electric and magnetic fields that propagate through space at the speed of light, c. The waves are transverse: the fields oscillate in a direction perpendicular to the direction of wave propagation. Unpolarized light consists of a superposition of many light waves that have their electric and magnetic field vectors pointing in random directions perpendicular to the wave propagation. Since the magnitude of the magnetic field is small compared to the electric field, it is the electric field that interacts with matter most strongly. Polarizing filters are typically made of plastic that contains tiny crystals arranged in the same direction so that they transmit only the component of the electric field parallel to the direction of alignment; the perpendicular component of the electric field is absorbed. Each electric field vector can be resolved to a component that is parallel and a component that is perpendicular to the polarizing axis. The parallel component will pass through the filter and the perpendicular component will be absorbed. Since the electric field vectors are randomly aligned in unpolarized light, half of the light intensity corresponds to the electric field components parallel to the polarizing axis. Therefore, the photometer between the filters will read one half i . Malus's law can be used to find the amount of light transmitted through the second filter. The intensity of transmitted light is I subscript t equals I subscript zero cosine squared theta , where I subscript zero is the intensity of the polarized beam between the two filters and theta is the angle between the two polarizing axes. Since theta equals 60 degrees; and cosine 60 degrees; equals one half , cosine squared theta equals one fourth, and I subscript zero equals one half i, the second photometer will register an intensity of one half i times one fourth equals one eighth i.
.
Correct Response: D. (Objective 0014) Electromagnetic waves consist of oscillating electric and magnetic fields that propagate through space at the speed of light, c. The waves are transverse: the fields oscillate in a direction perpendicular to the direction of wave propagation. Unpolarized light consists of a superposition of many light waves that have their electric and magnetic field vectors pointing in random directions perpendicular to the wave propagation. Since the magnitude of the magnetic field is small compared to the electric field, it is the electric field that interacts with matter most strongly. Polarizing filters are typically made of plastic that contains tiny crystals arranged in the same direction so that they transmit only the component of the electric field parallel to the direction of alignment; the perpendicular component of the electric field is absorbed. Each electric field vector can be resolved to a component that is parallel and a component that is perpendicular to the polarizing axis. The parallel component will pass through the filter and the perpendicular component will be absorbed. Since the electric field vectors are randomly aligned in unpolarized light, half of the light intensity corresponds to the electric field components parallel to the polarizing axis. Therefore, the photometer between the filters will read one half i . Malus's law can be used to find the amount of light transmitted through the second filter. The intensity of transmitted light is I subscript t equals I subscript zero cosine squared theta , where I subscript zero is the intensity of the polarized beam between the two filters and theta is the angle between the two polarizing axes. Since theta equals 60 degrees; and cosine 60 degrees; equals one half , cosine squared theta equals one fourth, and I subscript zero equals one half i, the second photometer will register an intensity of one half i times one fourth equals one eighth i.
Question 23
23. The diagram below shows two monochromatic, coherent light sources that are separated by a small distance d. Light from the two sources strikes the screen at point A. The light sources are located at distances of s1 subscript 1 and s2 subscript 2 from point A.
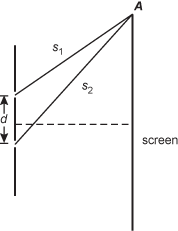
The two light sources converge on a screen parallel to the sources at one point A.
Which of the following best explains the necessary condition for point A on the screen to be a region of maximum light intensity?
- when the ratio of d to s1 subscript 1 equals λ lambda
- when d is of the same order of magnitude as λ lambda
- when the sum of d and s1 subscript 1 is equal to s2 subscript 2
- when the difference between s2 subscript 2 and s1 subscript 1 is an integral multiple of λ lambda
Answer to question 23
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0014) The light waves are monochromatic, so they all have the same wavelength. The light is also coherent, which means that the light from each source is in phase. According to the superposition principle, two light waves that travel along paths s1 and s2 will add when they arrive at point A. If the waves add constructively, there will be a bright band on the screen. If the waves add destructively, there will be a dark band (no light) on the screen. Since the waves are in phase, they will add constructively if the wave amplitudes are aligned. This will occur when the difference in the length of the paths taken (s2–s1) is an integral multiple of the wavelength. The waves will add destructively if the path lengths differ by one-half of a wavelength.
Correct Response: D. (Objective 0014) The light waves are monochromatic, so they all have the same wavelength. The light is also coherent, which means that the light from each source is in phase. According to the superposition principle, two light waves that travel along paths s subscript one and s subscript two will add when they arrive at point A. If the waves add constructively, there will be a bright band on the screen. If the waves add destructively, there will be a dark band (no light) on the screen. Since the waves are in phase, they will add constructively if the wave amplitudes are aligned. This will occur when the difference in the length of the paths taken open parenthesis s subscript two minus s subscript one close parenthesisis an integral multiple of the wavelength. The waves will add destructively if the path lengths differ by one half of a wavelength.
Question 24
24. Light from a laser passes through a single slit of width a, creating the light pattern shown below.
The largest is in the center, and is labeled with a width of delta y. Two equivalent midsized ovals are on either side, and outer most are two equivalent small ovals.
For which color of laser light will Δ Delta y be greatest?
- red
- yellow
- green
- blue
Answer to question 24
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0014) For a single slit, the regions in which the light intensity is minimum are given by d sin θ = mλ , where d is the width of the slit, θ is the angular displacement of the beam, m is the order of the minimum, and λ is the wavelength. The distance Δy corresponds to the distance between the first two minimums when m = 1. From this it follows that Δy will increase as the wavelength of the light increases—the longer the wavelength of light, the greater the distance between the first two minimums. Of the choices given, red light has the longest wavelength.
Correct Response: A. (Objective 0014) For a single slit, the regions in which the light intensity is minimum are given by d sine theta equals m times lambda, where d is the width of the slit, theta is the angular displacement of the beam, m is the order of the minimum, and lambda is the wavelength. The distance delta times y corresponds to the distance between the first two minimums when m equals 1. From this it follows that delta times y will increase as the wavelength of the light increases—the longer the wavelength of light, the greater the distance between the first two minimums. Of the choices given, red light has the longest wavelength.
Question 25
25. Which of the following characteristics describes the structure of material used in a fabricating a linear transmission polarizing filter?
- high refractive index producing total internal reflection of the magnetic field component of an electromagnetic wave
- a film containing long-chain molecules that selectively absorb or absorb and re-emit the electric field component of an electromagnetic wave
- doped semiconductor element arranged with adjacent P and N type regions that support an electric field
- a transparent film with parallel opaque lines produced by high-power laser light and having micrometer separation distances
Answer to question 25
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0014) Light produced by the sun and common lightbulbs is created by vibrating electric charges. The process creates an electromagnetic wave consisting of an electric field component and a magnetic field component that are perpendicular to each other. Typically the charges producing this wave are vibrating in random directions and, thus, generate electromagnetic wave components that also randomly vary in the direction perpendicular to the direction of the wave propagation. This is called unpolarized light. Polarized light consists of light waves in which the vibrations occur in a single plane, resulting in both the electric and magnetic fields having defined orientations. Polarization can occur through the processes of reflection, refraction, and transmission, and as a result of scattering. A polarizing filter is a material that incorporates long-chain molecules in its chemical structure that selectively absorb or pass wave energy depending on orientation. After passing through a single filter of this type, light is plane-polarized, with the electric field component having a defined direction. The addition of a second filter in the light path can produce a range of results depending on the orientation of the filters: minimal additional absorption when the orientation of the two materials is zero degrees to total absorption when the filter materials are at 90 degrees to each other.
Correct Response: B. (Objective 0014) Light produced by the sun and common lightbulbs is created by vibrating electric charges. The process creates an electromagnetic wave consisting of an electric field component and a magnetic field component that are perpendicular to each other. Typically the charges producing this wave are vibrating in random directions and, thus, generate electromagnetic wave components that also randomly vary in the direction perpendicular to the direction of the wave propagation. This is called unpolarized light. Polarized light consists of light waves in which the vibrations occur in a single plane, resulting in both the electric and magnetic fields having defined orientations. Polarization can occur through the processes of reflection, refraction, and transmission, and as a result of scattering. A polarizing filter is a material that incorporates long-chain molecules in its chemical structure that selectively absorb or pass wave energy depending on orientation. After passing through a single filter of this type, light is plane-polarized, with the electric field component having a defined direction. The addition of a second filter in the light path can produce a range of results depending on the orientation of the filters: minimal additional absorption when the orientation of the two materials is zero degrees to total absorption when the filter materials are at 90 degrees to each other.
Question 26
26. A certain ideal gas has a heat capacity at constant volume of Cv subscript v = 12.5 J/(mol•K)joules per mole kelvin. One mole of the gas in a cylinder absorbs 1000 J of heat and does 400 J of work while expanding. If the initial temperature of the gas is 300 K, what is the approximate final temperature of the gas?
- 316 K
- 324 K
- 332 K
- 348 K
Answer to question 26
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0015) The first law of thermodynamics is ΔE = Q − W where ΔE is the change in internal energy of the system, Q is the heat added to the system which is 1000 J, and W is the work done by the gas, or 400 J. Putting in the values gives ΔE = 600 J. In addition, ΔE = nCvΔT where n is the number of moles of the gas which is given as 1 mol, and ΔT is the change in temperature of the gas. Therefore ΔE = nCvΔT = 600 J, which becomes (12.5 J/K)ΔT = 600 J which results in ΔT = 48 K, so T final is 348 K.
Correct Response: D. (Objective 0015) The first law of thermodynamics is Delta E equals Q minus W where Delta E is the change in internal energy of the system, Q is the heat added to the system which is 1000 J, and W is the work done by the gas, or 400 J. Putting in the values gives Delta E equals 600 J. In addition, Delta E equals nC subscript v Delta T where n is the number of moles of the gas which is given as 1 mole, and Delta T is the change in temperature of the gas. Therefore Delta E equals nC subscript v Delta T equals 600 J, which becomes (12.5 joules per kelvin) Delta T equals 600 J which results in Delta T equals 48 K, so T final is 348 K.
Question 27
27. A heat engine consists of 1.0 mol of an ideal gas operating in a Carnot cycle. In state I in the graph below, the gas has a pressure of 20,000 Pa and a volume of 0.50 m3. In state III the gas has a pressure of 5,000 Pa and a volume of 1.0 m3.
Four points labelled I, II, III, and IV are connected in a non intersecting, continuous cycle of roughly parallelogram shape. Point I has lowest V and highest P. Point II has a higher V and lower P. Point III has the highest V and the lowest P. Point IV has a lower V and higher P.
What is the efficiency of the heat engine?
- 20%
- 30%
- 50%
- 70%
Answer to question 27
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0015) The efficiency of a heat engine operating between two heat reservoirs, Th and Tc, is given by
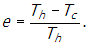 Since the processes from I to II and from III to IV are isothermals, the temperature of the gas in state I and state III is the temperature of the heat reservoirs and can be found using the ideal gas law, PV = nRT, where R = 8.31 J/mol-K. It follows that
Since the processes from I to II and from III to IV are isothermals, the temperature of the gas in state I and state III is the temperature of the heat reservoirs and can be found using the ideal gas law, PV = nRT, where R = 8.31 J/mol-K. It follows that
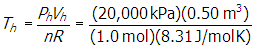 = 1,203 K,
= 1,203 K,
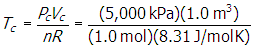 = 601.7 K, and the efficiency is e = 50%.
Correct Response: C. (Objective 0015) The efficiency of a heat engine operating between two heat reservoirs, T subscript h and T subscript c, is given by e equals start fraction numerator t sub h baseline minus t subscript c denominator t subscript h end fraction. Since the processes from I to II and from III to IV are isothermals, the temperature of the gas in state I and state III is the temperature of the heat reservoirs and can be found using the ideal gas law, P V equals n R T, where R equals 8.31 J slash mol K. It follows that t subscript h equals start fraction numerator p subscript h baseline v subscript h denominator n r end fraction equals start fraction numerator open parenthesis twenty thousand k upper p a close parenthesis open parenthesis zero point five zero m cubed close parenthesis denominator open parenthesis one point zero mol close parenthesis open parenthesis eight point three one j slash mol k close parenthesis end fraction equals 1,203 K, t subscript c equals start fraction numerator p subscript c baseline v subscript c denominator n r end fraction equals start fraction numerator open parenthesis five thousand k upper p a close parenthesis open parenthesis one point zero m cubed close parenthesis denominator open parenthesis one point zero mol close parenthesis open parenthesis eight point three one j slash mol k close parenthesis end fraction equals 601.7 K, and the efficiency is e equals fifty percent.
= 601.7 K, and the efficiency is e = 50%.
Correct Response: C. (Objective 0015) The efficiency of a heat engine operating between two heat reservoirs, T subscript h and T subscript c, is given by e equals start fraction numerator t sub h baseline minus t subscript c denominator t subscript h end fraction. Since the processes from I to II and from III to IV are isothermals, the temperature of the gas in state I and state III is the temperature of the heat reservoirs and can be found using the ideal gas law, P V equals n R T, where R equals 8.31 J slash mol K. It follows that t subscript h equals start fraction numerator p subscript h baseline v subscript h denominator n r end fraction equals start fraction numerator open parenthesis twenty thousand k upper p a close parenthesis open parenthesis zero point five zero m cubed close parenthesis denominator open parenthesis one point zero mol close parenthesis open parenthesis eight point three one j slash mol k close parenthesis end fraction equals 1,203 K, t subscript c equals start fraction numerator p subscript c baseline v subscript c denominator n r end fraction equals start fraction numerator open parenthesis five thousand k upper p a close parenthesis open parenthesis one point zero m cubed close parenthesis denominator open parenthesis one point zero mol close parenthesis open parenthesis eight point three one j slash mol k close parenthesis end fraction equals 601.7 K, and the efficiency is e equals fifty percent.
Question 28
28. If the pressure of an ideal gas is doubled while the volume of the gas remains constant, then the average speed of the molecules will increase by a factor of:
-
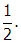 one half
one half
-
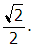 square root of two over two
square root of two over two
- √2 square root of 2 .
- 2.
Answer to question 28
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0015) The average kinetic energy of the molecules in an ideal gas is proportional to the temperature of the gas. If the pressure of the gas is doubled while the volume remains constant, the temperature can be found using the idea gas law, PV = nRT. Since n, R, and V are constant, then
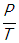 = constant and
= constant and
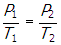 ,
,
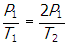 , and T2 = 2T1; that is, the temperature doubles. Since temperature is proportional to the average kinetic energy of the molecules,
, and T2 = 2T1; that is, the temperature doubles. Since temperature is proportional to the average kinetic energy of the molecules,
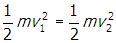 ,
,
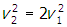 , and v2 = √2v1. Thus, the average speed of the molecules increases by a factor of √2.
Correct Response: C. (Objective 0015) The average kinetic energy of the molecules in an ideal gas is proportional to the temperature of the gas. If the pressure of the gas is doubled while the volume remains constant, the temperature can be found using the idea gas law, P V equals n R T. Since n, R, and V are constant, then p over t equals constant and p subscript one over t subscript one equals p subscript two over t subscript two, p subscript one over t subscript one equals p subscript two over t subscript two, p subscript one over t subscript one equals two p subscript one over t subscript two, and T subscript 2 equals 2 T subscript 1; that is, the temperature doubles. Since temperature is proportional to the average kinetic energy of the molecules, one half m v subscript one baseline squared equals one half m v subscript two baseline squared, v subscript two baseline squared equals two v subscript one baseline squared, and v subscript two equals square root of 2 v subscript one Thus, the average speed of the molecules increases by a factor of square root of 2.
, and v2 = √2v1. Thus, the average speed of the molecules increases by a factor of √2.
Correct Response: C. (Objective 0015) The average kinetic energy of the molecules in an ideal gas is proportional to the temperature of the gas. If the pressure of the gas is doubled while the volume remains constant, the temperature can be found using the idea gas law, P V equals n R T. Since n, R, and V are constant, then p over t equals constant and p subscript one over t subscript one equals p subscript two over t subscript two, p subscript one over t subscript one equals p subscript two over t subscript two, p subscript one over t subscript one equals two p subscript one over t subscript two, and T subscript 2 equals 2 T subscript 1; that is, the temperature doubles. Since temperature is proportional to the average kinetic energy of the molecules, one half m v subscript one baseline squared equals one half m v subscript two baseline squared, v subscript two baseline squared equals two v subscript one baseline squared, and v subscript two equals square root of 2 v subscript one Thus, the average speed of the molecules increases by a factor of square root of 2.
Question 29
29. A 10 Ω ohm resistor is placed in an insulated calorimeter containing 0.25 kg of water at 20°C degrees celsius . The resistor is connected to a constant current source, and after 64 s the temperature of the water is 30°C degrees celsius . No heat is lost to the surroundings and the heat capacity of the calorimeter and resistor can be ignored. What is the current in the resistor?
- 4 A
- 8 A
- 16 A
- 32 A
Answer to question 29
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0015) As current passes through the resistor, heat is dissipated due to Joule heating. The power dissipated is P = IV, which can be combined with Ohm's law, V = IR, to get P = I2R. Since power is the rate of change of energy,
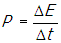 , multiplying the power by the time interval gives an expression for the energy dissipated, ΔE = ΔtI2R. By the first law of thermodynamics, this must equal the heat gained by the water, Q = cm ΔT. Setting these two expressions equal using c = 4.19 × 103 J/(kg-°C), substituting values, and solving for I results in I = 4 A.
Correct Response: A. (Objective 0015) As current passes through the resistor, heat is dissipated due to Joule heating. The power dissipated is P equals I V, which can be combined with Ohm's law, V equals I R, to get P equals I squared R. Since power is the rate of change of energy, p equals delta e over delta t, multiplying the power by the time interval gives an expression for the energy dissipated, delta E equals delta t I squared R. By the first law of thermodynamics, this must equal the heat gained by the water, Q equals cm delta T. Setting these two expressions equal using c equals 4.19 times 10 cubed J slash open parenthesis k g - degrees celsius close parenthesis, substituting values, and solving for I results in I equals 4 A.
, multiplying the power by the time interval gives an expression for the energy dissipated, ΔE = ΔtI2R. By the first law of thermodynamics, this must equal the heat gained by the water, Q = cm ΔT. Setting these two expressions equal using c = 4.19 × 103 J/(kg-°C), substituting values, and solving for I results in I = 4 A.
Correct Response: A. (Objective 0015) As current passes through the resistor, heat is dissipated due to Joule heating. The power dissipated is P equals I V, which can be combined with Ohm's law, V equals I R, to get P equals I squared R. Since power is the rate of change of energy, p equals delta e over delta t, multiplying the power by the time interval gives an expression for the energy dissipated, delta E equals delta t I squared R. By the first law of thermodynamics, this must equal the heat gained by the water, Q equals cm delta T. Setting these two expressions equal using c equals 4.19 times 10 cubed J slash open parenthesis k g - degrees celsius close parenthesis, substituting values, and solving for I results in I equals 4 A.
Question 30
30. A passive solar hot water heating system consists of a closed loop containing a working fluid circulating through an insulated water storage tank. The working fluid is 20 kg of a-propylene glycol. When the solar collector is exposed to sunlight, energy is transferred to the working fluid, causing its temperature to increase from 10°C degrees celsius to 70°C degrees celsius . If the specific heat capacity of propylene glycol mixture = 3.60 J/g•°C degrees celsius , how much energy does the working fluid absorb?
- 4.32 × times 103 to the power of 3 J
- 5.04 × times 103 to the power of 3 J
- 4.32 × times 106 to the power of 6 J
- 5.04 × times 106 to the power of 6 J
Answer to question 30
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0015) In this problem, solar energy provides heating to the working fluid in the system. The energy change in the working fluid is given by Q = mcΔt, where Q is in joules, m = mass of fluid in kilograms, c = specific heat of the fluid in cal/g•°C degrees celsius , and Δt is the temperature change in Celsius degrees. From this is follows that Q = (20 kg) × (3.60 × 103 J/kg•°C degrees celsius ) × (70°C degrees celsius − 10°C degrees celsius ) = 4320 × 103 J.
Correct Response: C. (Objective 0015) In this problem, solar energy provides heating to the working fluid in the system. The energy change in the working fluid is given by Q equals mc delta t, where Q is in joules, m equals mass of fluid in kilograms, c equals specific heat of the fluid in cal/g• degrees celsius, and delta t is the temperature change in celsius degrees. From this is follows that Q equals (20 kg) times (3.60 times 10 cubed J/kg• degrees celsius) times (70 degrees celsius minus 10 degrees celsius) equals 4320 times 10 cubed J.
Question 31
31. A Geiger counter placed near a radioactive source registers 80 counts per minute when adjusted for background radiation. When a piece of paper is placed between the source and the Geiger counter window, the number drops to 0 counts per minute. This indicates that the source is emitting:
- alpha particles only.
- beta particles only.
- gamma particles only.
- beta and gamma particles only.
Answer to question 31
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0016) A Geiger counter measures ionizing radiation. Most radioactive sources emit alpha, beta, or gamma radiation. Of these types of radiation, alpha particles have the lowest energy and consist of two protons and two neutrons. These particles are generally stopped by a piece of paper. Beta particles are electrons emitted by the nucleus and have greater energy. These particles are usually stopped by a sheet of aluminum foil. Gamma particles are high-energy photons that can only be stopped by a thick sheet of lead or a large slab of concrete. Since the number registered by the Geiger counter dropped to 0 counts per minute when a piece of paper was placed between the window of the counter and the source, the source is emitting only alpha particles.
Correct Response: A. (Objective 0016) A Geiger counter measures ionizing radiation. Most radioactive sources emit alpha, beta, or gamma radiation. Of these types of radiation, alpha particles have the lowest energy and consist of two protons and two neutrons. These particles are generally stopped by a piece of paper. Beta particles are electrons emitted by the nucleus and have greater energy. These particles are usually stopped by a sheet of aluminum foil. Gamma particles are high-energy photons that can only be stopped by a thick sheet of lead or a large slab of concrete. Since the number registered by the Geiger counter dropped to 0 counts per minute when a piece of paper was placed between the window of the counter and the source, the source is emitting only alpha particles.
Question 32
32. The reaction below shows the radioactive decay of potassium-40 into calcium-40 and an unidentified particle, X.
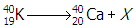
What is the identity of X in this reaction?
- a positron
- a beta particle
- a proton
- an alpha particle
Answer to question 32
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0016) According to the reaction, the number of protons in the nucleus of the potassium atom increases by one while the atomic mass remains the same. Therefore, a neutron must have decayed into a proton and an electron. This is known as beta decay, and beta particles
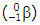 are electrons that arise from the decay of a neutron into a proton and an electron. Emission of a beta particle from a radioisotope will increase the number of protons in the nucleus by one and decrease the number of neutrons by one, maintaining the same number of nucleons.
Correct Response: B. (Objective 0016) According to the reaction, the number of protons in the nucleus of the potassium atom increases by one while the atomic mass remains the same. Therefore, a neutron must have decayed into a proton and an electron. This is known as beta decay, and beta particles open parenthesis beta with a mass of zero and an atomic number of negative one close parenthesis are electrons that arise from the decay of a neutron into a proton and an electron. Emission of a beta particle from a radioisotope will increase the number of protons in the nucleus by one and decrease the number of neutrons by one, maintaining the same number of nucleons.
are electrons that arise from the decay of a neutron into a proton and an electron. Emission of a beta particle from a radioisotope will increase the number of protons in the nucleus by one and decrease the number of neutrons by one, maintaining the same number of nucleons.
Correct Response: B. (Objective 0016) According to the reaction, the number of protons in the nucleus of the potassium atom increases by one while the atomic mass remains the same. Therefore, a neutron must have decayed into a proton and an electron. This is known as beta decay, and beta particles open parenthesis beta with a mass of zero and an atomic number of negative one close parenthesis are electrons that arise from the decay of a neutron into a proton and an electron. Emission of a beta particle from a radioisotope will increase the number of protons in the nucleus by one and decrease the number of neutrons by one, maintaining the same number of nucleons.
Question 33
33. According to the standard model, which of the following best describes the mechanism of the strong, weak, and electromagnetic interactions?
- The interactions generate energy through the decay of dark matter.
- The interactions result from the exchange of bosons between particles.
- The interactions are a manifestation of gravity in different reference frames.
- The interactions are produced by the pairing of quarks and antiquarks.
Answer to question 33
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0016) The standard model describes the strong, weak, and electromagnetic interactions as forces that are mediated by the exchange of particles called bosons. The photon is an example of a boson, and it mediates the electromagnetic force.
Correct Response: B. (Objective 0016) The standard model describes the strong, weak, and electromagnetic interactions as forces that are mediated by the exchange of particles called bosons. The photon is an example of a boson, and it mediates the electromagnetic force.
Question 34
34. A GPS (global positioning system) satellite has an orbital speed of about 14,000 kg/hr, or 3,889 m/s. According to the theory of special relativity, compared to the stationary clock on the earth, the clock in the satellite will measure a second as being:
- longer and therefore run slow.
- longer and therefore run fast.
- shorter and therefore run slow.
- shorter and therefore run fast.
Answer to question 34
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0016) According to the theory of special relativity, a clock in an inertial reference frame moving at a constant speed with respect to a clock in a stationary reference frame will undergo time dilation. This means that a second measured in the moving clock will be slightly longer than a second measured in the stationary clock. This will result in the clock in the satellite running more slowly than the clock in the stationary frame.
Correct Response: A. (Objective 0016) According to the theory of special relativity, a clock in an inertial reference frame moving at a constant speed with respect to a clock in a stationary reference frame will undergo time dilation. This means that a second measured in the moving clock will be slightly longer than a second measured in the stationary clock. This will result in the clock in the satellite running more slowly than the clock in the stationary frame.
Question 35
35. Which of the following statements best describes the role of the gluon in the standard model of physics?
- the force-carrying particle for the electromagnetic force
- a type of neutrino released by beta decay of a proton to a neutron
- the force-carrying particle for the nuclear strong force
- a particle that emerges due to quantum excitations in the Higgs field
Answer to question 35
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0016) Each of the fundamental forces has an associated force-carrying particle associated with it called gauge bosons. The nuclear strong force is carried by gluons. This is the force responsible for holding the atomic nucleolus together.
Correct Response: C. (Objective 0016) Each of the fundamental forces has an associated force-carrying particle associated with it called gauge bosons. The nuclear strong force is carried by gluons. This is the force responsible for holding the atomic nucleolus together.
Question 36
36. Which of the following best characterizes a basic property of semiconductors?
- Electrons in a semiconductor are free to scatter from atom to atom, resulting in a low value of conductivity.
- Semiconductors contain a region where the valence band energies overlap with the conduction band.
- Electrons in the atoms are paired with electron holes that pass through the material with almost zero resistance.
- Electrons with sufficient energy can transition a narrow energy gap between the valence band and the conduction band.
Answer to question 36
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0017) The band structure of a semiconductor is similar to that of an insulator. They both have bands that are completely full at absolute zero temperature and an empty band above the topmost filled band. The difference is that in a semiconductor the energy gap between the topmost filled band, called the valence band, and the next highest band, called the conduction band, is small enough that at room temperature thermal agitation allows some electrons to jump the energy gap from the valence band into the conduction band. Electron states in the valence band that are empty because they are missing their electrons are called holes. Both electrons in the conduction band and holes in the valence band contribute to the electrical conductivity of a semiconductor.
Correct Response: D. (Objective 0017) The band structure of a semiconductor is similar to that of an insulator. They both have bands that are completely full at absolute zero temperature and an empty band above the topmost filled band. The difference is that in a semiconductor the energy gap between the topmost filled band, called the valence band, and the next highest band, called the conduction band, is small enough that at room temperature thermal agitation allows some electrons to jump the energy gap from the valence band into the conduction band. Electron states in the valence band that are empty because they are missing their electrons are called holes. Both electrons in the conduction band and holes in the valence band contribute to the electrical conductivity of a semiconductor.
Question 37
37. An arrangement of electric and magnetic fields is used as a velocity selector to determine the speed, v, of an electron of mass m moving in one dimension. The speed of the electron can be determined with an accuracy of ± plus or minus 10% of v. Which of the following gives the uncertainty in the position of the electron?
-
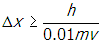
-
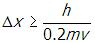
-
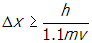
-
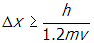
Answer to question 37
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0017) The uncertainty principle expresses a relationship between measuring the momentum and position of a particle simultaneously. One form of the relationship states that ΔxΔp ≥ h. Since the accuracy in the speed, v, of the electron is 10%, then the uncertainty in the electron's speed is Δv = (v + 0.1v) − (v − 0.1v) = 0.2v. Since p = mv, Δp = mΔv. Substituting this into the uncertainly principle and solving for Δx gives
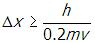 .
Correct Response: B. (Objective 0017) The uncertainty principle expresses a relationship between measuring the momentum and position of a particle simultaneously. One form of the relationship states that delta x delta p greater then or equal to h. Since the accuracy in the speed, v, of the electron is ten percent, then the uncertainty in the electron's speed is delta v equals open parenthesis v plus 0.1 v close parenthesis minus open parenthesis v minus 0.1 v close parenthesis equals 0.2 v. Since p equals m v, delta p equals m delta v. Substituting this into the uncertainly principle and solving for delta x gives delta x greater than or equals to start fraction numerator h denominator zero point two m v end fraction.
.
Correct Response: B. (Objective 0017) The uncertainty principle expresses a relationship between measuring the momentum and position of a particle simultaneously. One form of the relationship states that delta x delta p greater then or equal to h. Since the accuracy in the speed, v, of the electron is ten percent, then the uncertainty in the electron's speed is delta v equals open parenthesis v plus 0.1 v close parenthesis minus open parenthesis v minus 0.1 v close parenthesis equals 0.2 v. Since p equals m v, delta p equals m delta v. Substituting this into the uncertainly principle and solving for delta x gives delta x greater than or equals to start fraction numerator h denominator zero point two m v end fraction.
Question 38
38. The electron energy level diagram for an atom consisting of a single electron that is only allowed to occupy three states is shown below.

Vertical line with three arms coming out to the left. starting at the bottom we have n equals one then a large distance up to n equals two then a short distance up to n equals three
Which of the following must be known in order to calculate the frequency of the lines in the emission spectrum of this atom?
- the spin of the electron in each state
- the energy difference between the states
- the ground state energy of the electron
- the uncertainty in momentum of the electron in each state
Answer to question 38
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0017) The atomic spectrum of an isotope is generated by electrons in an atom undergoing transitions from one energy state to another. For example, the frequency of light emitted as the electron transitions from the n = 3 excited state to the n = 2 excited state can be calculated using the equation E3 − E2 = hf. Since the value of Planck's constant (h) is known, the frequency, f, can be determined for each of the three possible electron transitions if the energy difference between the states is known.
Correct Response: B. (Objective 0017) The atomic spectrum of an isotope is generated by electrons in an atom undergoing transitions from one energy state to another. For example, the frequency of light emitted as the electron transitions from the n equals 3 excited state to the n equals 2 excited state can be calculated using the equation E subscript three minus E subscript two equals h f. Since the value of Planck's constant (h) is known, the frequency, f, can be determined for each of the three possible electron transitions if the energy difference between the states is known.
Question 39
39. A scientist performs an experiment with a microscope that uses photons to determine the position of an electron. The electron is in a potential well of width L, where L is of the order of magnitude of the diameter of an atom. The scientist starts with electromagnetic radiation of wavelength λ = L and progressively uses radiation of smaller and smaller wavelengths. Which of the following best describes what will occur as the size of the wavelength decreases?
- The energy of the incident photons will decrease.
- The de Broglie wavelength of the electron will increase.
- The electron will drop to lower energy levels in the well.
- The momentum of the photons will disturb the electron's position.
Answer to question 39
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0017) Photons have momentum, and when they interact with an electron through a collision, some of the momentum will be transferred to the electron, further disturbing its position. The momentum of a photon is given by
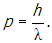 As the wavelength of the photons decreases, the momentum of the photons increases. These photons will scatter off the electron and disturb its position.
Correct Response: D. (Objective 0017) Photons have momentum, and when they interact with an electron through a collision, some of the momentum will be transferred to the electron, further disturbing its position. The momentum of a photon is given by p equals h over lambda. As the wavelength of the photons decreases, the momentum of the photons increases. These photons will scatter off the electron and disturb its position.
As the wavelength of the photons decreases, the momentum of the photons increases. These photons will scatter off the electron and disturb its position.
Correct Response: D. (Objective 0017) Photons have momentum, and when they interact with an electron through a collision, some of the momentum will be transferred to the electron, further disturbing its position. The momentum of a photon is given by p equals h over lambda. As the wavelength of the photons decreases, the momentum of the photons increases. These photons will scatter off the electron and disturb its position.
Question 40
40. A peak emission line from an ionized sample of gas has a wavelength of 588 nm. Which of the following differences in electron energy level is responsible for producing this line?
- 3.38 × times 10–19to the power of negative 19 eV
- 2.11 × times 10–3to the power of negative 3 eV
- 2.11 eV
- 3.38 eV
Answer to question 40
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0017) The relationship between energy level differences and peak wavelengths for emission spectra is given by
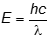 where E = energy in joules, h = Plank's constant, 6.63 × 10–34 J•s, λ = wavelength of the emission line in meters, and c = speed of light, 3 × 108 m/s. Solving for E gives: E = ((6.63 × 10–34 J•s)(3.00 × 108 m/s))/(588 × 10–9 m) = 3.38 × 10–19 joules. Converting from joules to electron volts: 1 eV = 1.60 × 10–19 joules, thus E = (3.38 × 10–19 joules / 1.60 × 10–19 joules/eV) = 2.11 eV.
Correct Response: C. (Objective 0017) The relationship between energy level differences and peak wavelengths for emission spectra is given by E equals h c over lamba where E = energy in joules, h = Plank's constant, 6.63 times 10 to the power of negative 34 J•s, lambda = wavelength of the emission line in meters, and c = speed of light, 3 times 10 to the power of 8 m/s. Solving for E gives: E = ((6.63 times 10 to the power of negative 34 J•s)(3.00 times 10 to the power of 8 m/s))/(588 times 10 to the power of negative 9 m) = 3.38 times 10 to the power of negative 19 joules. Converting from joules to electron volts: 1 eV = 1.60 times 10 to the power of negative 19 joules, thus E = (3.38 times 10 to the power of negative 19 joules / 1.60 times 10 to the power of negative 19 joules/eV) = 2.11 eV.
where E = energy in joules, h = Plank's constant, 6.63 × 10–34 J•s, λ = wavelength of the emission line in meters, and c = speed of light, 3 × 108 m/s. Solving for E gives: E = ((6.63 × 10–34 J•s)(3.00 × 108 m/s))/(588 × 10–9 m) = 3.38 × 10–19 joules. Converting from joules to electron volts: 1 eV = 1.60 × 10–19 joules, thus E = (3.38 × 10–19 joules / 1.60 × 10–19 joules/eV) = 2.11 eV.
Correct Response: C. (Objective 0017) The relationship between energy level differences and peak wavelengths for emission spectra is given by E equals h c over lamba where E = energy in joules, h = Plank's constant, 6.63 times 10 to the power of negative 34 J•s, lambda = wavelength of the emission line in meters, and c = speed of light, 3 times 10 to the power of 8 m/s. Solving for E gives: E = ((6.63 times 10 to the power of negative 34 J•s)(3.00 times 10 to the power of 8 m/s))/(588 times 10 to the power of negative 9 m) = 3.38 times 10 to the power of negative 19 joules. Converting from joules to electron volts: 1 eV = 1.60 times 10 to the power of negative 19 joules, thus E = (3.38 times 10 to the power of negative 19 joules / 1.60 times 10 to the power of negative 19 joules/eV) = 2.11 eV.