Physics (Grades 9–12)
Subtest 1 Sample Items
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Expand All | Collapse All
Question 1
1. The experiment below has been designed to test the idea that a car will have greater fuel efficiency with narrower tires than with standard-sized tires due to a reduction in the amount of friction with the driving surface.
- The car will first be driven with tires that are 80% of the width of standard tires. Then the car will be driven with standard-width tires.
- The car will be tested on a closed driving course.
- The car's miles per gallon with each type of tire will be calculated and compared.
Which of the following additional criteria is most important to include in this experimental design?
- The frictional forces acting on the car will be measured.
- The test runs will be made under identical conditions.
- The test drives should simulate actual driving environments.
- The data will be collected real-time using digital data sensors.
Answer to question 1
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0001) In the experiment described above, the variables are the width of the tires and the car's gas mileage (its fuel efficiency). The width of the tires is the independent variable and the gas mileage is the dependent variable. To determine whether the width of the tires affects the gas mileage, it is essential that other factors that could affect the gas mileage, such as the speed at which the car is driven, the weather conditions, and the air pressure in the tires, are kept constant and not allowed to vary. If the test runs are made under identical conditions, then the researchers can be certain that any differences in gas mileage are due only to the difference in the width of the tires used.
Correct Response: B. (Objective 0001) In the experiment described above, the variables are the width of the tires and the car's gas mileage (its fuel efficiency). The width of the tires is the independent variable and the gas mileage is the dependent variable. To determine whether the width of the tires affects the gas mileage, it is essential that other factors that could affect the gas mileage, such as the speed at which the car is driven, the weather conditions, and the air pressure in the tires, are kept constant and not allowed to vary. If the test runs are made under identical conditions, then the researchers can be certain that any differences in gas mileage are due only to the difference in the width of the tires used.
Question 2
2. Students are performing the following phase change experiment.
- Apply a constant controlled heat source to a mixture of ice and water in a beaker.
- Use a thermometer to monitor and record the temperature of the contents of the beaker every three minutes.
- Continue applying heat and recording the temperature until most of the ice and water has been converted into water vapor.
Which of the following approaches would be most helpful in analyzing the data collected during this experiment?
- finding the regression line relating temperature and time
- graphing the relationship between temperature and time
- determining the median temperature of the data set
- finding the standard deviation of the temperature in the data set
Answer to question 2
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0001) As heat is applied to the ice and water mixture, the temperature will remain constant until all of the ice has melted. Once the ice has melted, the temperature of the water will increase at an approximately constant rate until it reaches the boiling point. As the water boils and is converted to steam, it will remain at that constant temperature. The most helpful way to analyze the data to see this behavior is to graph the temperature versus time. The graph will display a horizontal line until the ice has melted, then a slanted line, and again a horizontal line as the water boils. This demonstrates that temperature remains constant during a phase change (if the pressure is constant).
Correct Response: B. (Objective 0001) As heat is applied to the ice and water mixture, the temperature will remain constant until all of the ice has melted. Once the ice has melted, the temperature of the water will increase at an approximately constant rate until it reaches the boiling point. As the water boils and is converted to steam, it will remain at that constant temperature. The most helpful way to analyze the data to see this behavior is to graph the temperature versus time. The graph will display a horizontal line until the ice has melted, then a slanted line, and again a horizontal line as the water boils. This demonstrates that temperature remains constant during a phase change (if the pressure is constant).
Question 3
3. Students in the physics lab are exploring the properties of dry ice. Which of the following safety rules is most important to follow during these activities?
- Do not handle dry ice with bare hands.
- Perform all work with dry ice under a fume hood.
- Keep dry ice away from any open flame.
- Do not allow dry ice to come in contact with water.
Answer to question 3
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: A. (Objective 0001) Dry ice is a solid form of carbon dioxide that is extremely cold—around −79°C (−109°F). Because it is so cold, it can freeze the water in the skin cells when it comes in contact with bare skin, forming ice crystals that damage the cells. This creates a sensation similar to that of a burn caused by a hot substance and can be quite painful. Therefore, dry ice should not be handled with bare hands.
Correct Response: A. (Objective 0001) Dry ice is a solid form of carbon dioxide that is extremely cold—around negative 79 degrees celsius open parenthesis negative 109 degrees fahrenheit. Because it is so cold, it can freeze the water in the skin cells when it comes in contact with bare skin, forming ice crystals that damage the cells. This creates a sensation similar to that of a burn caused by a hot substance and can be quite painful. Therefore, dry ice should not be handled with bare hands.
Question 4
4. A physics lab involves measuring the speed of light using a pulsed laser beam and a mirror. A pulsed beam is sent down a long corridor, where it strikes a mirror and is reflected back to a sensor. The same beam is sent directly to the sensor, and the goal is to measure the time delay between the two signals. Which of the following instruments would be most appropriate for use in analyzing the electrical output from light sensors to determine the time delay associated with the two signals?
- photo gate
- oscilloscope
- voltmeter
- photometer
Answer to question 4
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0001) An oscilloscope is a laboratory instrument that converts electrical signals into visual waveforms displayed on a screen. Waveforms are represented with the y-axis representing voltage and the x-axis representing time. Oscilloscopes typically incorporate at least two inputs, allowing the simultaneous viewing of two signals. To measure the speed of light, the direct signal and the reflected signal are displayed on the oscilloscope. By reading and interpreting the calibrated time axis for the two channels, the user can determine the time delay interval.
Correct Response: B. (Objective 0001) An oscilloscope is a laboratory instrument that converts electrical signals into visual waveforms displayed on a screen. Waveforms are represented with the y-axis representing voltage and the x-axis representing time. Oscilloscopes typically incorporate at least two inputs, allowing the simultaneous viewing of two signals. To measure the speed of light, the direct signal and the reflected signal are displayed on the oscilloscope. By reading and interpreting the calibrated time axis for the two channels, the user can determine the time delay interval.
Question 5
5. A nonlinear spring is modeled by a force law given by F(x) = –10x + 3x2, where F is measured in newtons and x in meters. How much work is done stretching the spring to x = +2.0 m from its equilibrium position at x = 0.0 m?
5. A non linear spring is modeled by a force law of the form F of x equals minus ten x plus three x squared, where F is measured in newtons and x in meters. How much work is done stretching the spring to x equals positive two meters from its equilibrium position at x equals zero point zero meters?
- –7.0 N•m negative 7.0 newton meters
- –8.0 N•m negative 8.0 newton meters
- –12 N•m negative 12 newton meters
- –18 N•m negative 18 newton meters
Answer to question 5
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0002) Work for a constant force is W = F•d. The force in this question is not constant, so it is necessary to integrate the force over the displacement of the end of the spring. Since the force and displacement are in one dimension, the dot product can be evaluated by taking the components of the force and the displacements in a one-dimensional coordinate system. So
![W = the integral from 0 to 2 of F of x dx = [ negative 5 x squared + x cubed] evaluated 0 to 2](//www.mtle.nesinc.com/config/images/elements/MN064065/MN064_001_000002_0005_R.png) and thus W = –20 N•m + 8 N•m = –12 N•m.
Correct Response: C. (Objective 0002) Work for a constant force is W = F dot d. The force in this question is not constant, so it is necessary to integrate the force over the displacement of the end of the spring. Since the force and displacement are in one dimension, the dot product can be evaluated by taking the components of the force and the displacements in a one-dimensional coordinate system. So W = the integral from 0 to 2 of F of x dx = [ negative 5 x squared + x cubed] evaluated 0 to 2 and thus W = negative 20 newton meters + 8 newton meters = negative 12 newton meters.
and thus W = –20 N•m + 8 N•m = –12 N•m.
Correct Response: C. (Objective 0002) Work for a constant force is W = F dot d. The force in this question is not constant, so it is necessary to integrate the force over the displacement of the end of the spring. Since the force and displacement are in one dimension, the dot product can be evaluated by taking the components of the force and the displacements in a one-dimensional coordinate system. So W = the integral from 0 to 2 of F of x dx = [ negative 5 x squared + x cubed] evaluated 0 to 2 and thus W = negative 20 newton meters + 8 newton meters = negative 12 newton meters.
Question 6
6. A teacher is introducing students to the concept of vectors and gives them several problems similar to the one below.
Two forces, F1 subscript 1 and F2 subscript 2, act on mass m. F1 subscript 1 has a magnitude of 12 N and makes an angle of 30° degrees above the horizontal. F2 subscript 2 has a magnitude of 8 N and makes an angle of 60° degrees below the horizontal. What is the magnitude and direction of the net force on the mass?
The teacher would like to provide the students with a conceptual approach to thinking about and solving these problems while minimizing the amount of mathematical computation needed. Which of the following problem-solving strategies is most appropriate for meeting the teacher's goal?
- having students draw a scale diagram of the forces on the mass and measure with a ruler and protractor the magnitude and direction of the resultant force
- showing students how to solve systems of two equations in two unknowns using the addition method to eliminate one variable
- providing students with a mnemonic device to help them remember trigonometric relationships and allowing the use of calculators for computing their values
- showing students how the law of cosines and the law of sines can be used to solve the problems in place of the trigonometric ratios
Answer to question 6
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: A. (Objective 0002) The given problem deals with finding the magnitude and direction of the sum of two force vectors. While this type of problem can be solved using trigonometry, a more conceptual and less mathematical approach can also be used. Because forces are vectors, they can be represented geometrically using scale diagrams. The components of the vectors can be drawn and measured. A ruler can be used to measure the magnitude of the vector and a protractor can be used to determine its direction angle. Given two vectors drawn to scale with their appropriate direction angles, the vector sum can be found by either using the parallelogram rule or by finding the sum of each vector's x- and y-components.
Correct Response: A. (Objective 0001) (Objective 0002) The given problem deals with finding the magnitude and direction of the sum of two force vectors. While this type of problem can be solved using trigonometry, a more conceptual and less mathematical approach can also be used. Because forces are vectors, they can be represented geometrically using scale diagrams. The components of the vectors can be drawn and measured. A ruler can be used to measure the magnitude of the vector and a protractor can be used to determine its direction angle. Given two vectors drawn to scale with their appropriate direction angles, the vector sum can be found by either using the parallelogram rule or by finding the sum of each vector's x and y components.
Question 7
7. Which of the following is closest to the weight in newtons of an average adult?
- 10
N
- 500
N
- 1500
N
- 2500
N
Answer to question 7
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0002) The response choices make it clear that the question is asking for a rough estimate of the mass of an average adult. The newton is the SI unit of weight and is equal to 1 kilogram-meter/second2. To determine the weight of a person in newtons, his or her mass in kilograms is needed. To find this, remember that near the surface of the earth, the gravitational force on a 1.0 kg mass is equivalent to 2.2 pounds. Assuming that the average person weighs around 150 pounds, the mass of this person is 150 divided by 2.2, or about 68 or 70 kg. Multiplying this result by the acceleration of gravity, 9.8 m/s2, results in a weight of (70 kg)(9.8 m/s2) = 686 N, which is closest to 500 N.
Correct Response: B. (Objective 0002) The response choices make it clear that the question is asking for a rough estimate of the mass of an average adult. The newton is the
SI
unit of weight and is equal to 1 kilogram-meter per second squared. To determine the weight of a person in newtons, his or her mass in kilograms is needed. To find this, remember that near the surface of the earth, the gravitational force on a 1.0 kilograms mass is equivalent to 2.2 pounds. Assuming that the average person weighs around 150 pounds, the mass of this person is 150 divided by 2.2, or about 68 or 70 kilograms. Multiplying this result by the acceleration of gravity, 9.8 meter per second squared, results in a weight of open parenthesis 70 kilograms close parenthesis open parenthesis 9.8 meter per second squared close parenthesis equals 686 newtons, which is closest to 500 newtons.
Question 8
8. A student is analyzing the resistive force on a mass as it sinks in a fluid. The student assumes that the force is directly proportional to the product of the speed of the object (v), the cross-sectional area of the object (A), and the density of the fluid (ρ). What are the correct
SI
units for the constant of proportionality in the student's formula?
-
s-1 superscript negative 1
-
m-1 superscript negative 1
-
m/s
-
kg/s
Answer to question 8
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0002) Since the student assumes that the force on the mass as it sinks in a fluid is directly proportional to the product of the speed and cross-sectional area of the object and the density of the fluid, the formula can be written as F = cvAρ, where c is the constant of proportionality. To find the units for c, it is necessary to use dimensional analysis. Since the units on the left side of the equation must equal the units on the right side, substitute the SI units for each of the quantities in the equation and then determine, from inspection, the necessary units for c. The equation is
 . In order for the units on the right side of the equation to equal the units on the left side, the units for c must be m/s.
Correct Response: C. (Objective 0002) Since the student assumes that the force on the mass as it sinks in a fluid is directly proportional to the product of the speed and cross-sectional area of the object and the density of the fluid, the formula can be written as F equals c v A rho, where c is the constant of proportionality. To find the units for c, it is necessary to use dimensional analysis. Since the units on the left side of the equation must equal the units on the right side, substitute the S I units for each of the quantities in the equation and then determine, from inspection, the necessary units for c. The equation is start fraction numerator k g dash m denominator s squared end fraction equals c over one baseline times m over s basleine m squared over one baseline time k g over m cubed baseline equals c over one baseline times k g over s. In order for the units on the right side of the equation to equal the units on the left side, the units for c must be meters per second.
. In order for the units on the right side of the equation to equal the units on the left side, the units for c must be m/s.
Correct Response: C. (Objective 0002) Since the student assumes that the force on the mass as it sinks in a fluid is directly proportional to the product of the speed and cross-sectional area of the object and the density of the fluid, the formula can be written as F equals c v A rho, where c is the constant of proportionality. To find the units for c, it is necessary to use dimensional analysis. Since the units on the left side of the equation must equal the units on the right side, substitute the S I units for each of the quantities in the equation and then determine, from inspection, the necessary units for c. The equation is start fraction numerator k g dash m denominator s squared end fraction equals c over one baseline times m over s basleine m squared over one baseline time k g over m cubed baseline equals c over one baseline times k g over s. In order for the units on the right side of the equation to equal the units on the left side, the units for c must be meters per second.
Question 9
9. Students in a physics class are building simple LED circuits and learning about LED-based lightbulbs. A student asks the teacher how an LED produces light. Which of the following ideas would be most appropriate for the teacher to introduce to relate topics in contemporary physics to everyday life?
- polarization of photons
- electron energy transitions
- uncertainty principle
- statistical nature of entropy
Answer to question 9
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0002) Light-emitting diodes (LED) are built from semiconducting materials, which have a band gap between the valence band and the conducting band. When a current is applied to a semiconductor, some electrons move from the valence band to the conducting band. Electrons also pass back to the valence band. This is an electron transition from a higher energy (E2) to a lower energy level (E1). The transition results in a photon of energy E2 − E1 being released. The frequency of the photon is proportional to its energy.
Correct Response: B. (Objective 0002) Light-emitting diodes (L E D) are built from semiconducting materials, which have a band gap between the valence band and the conducting band. When a current is applied to a semiconductor, some electrons move from the valence band to the conducting band. Electrons also pass back to the valence band. This is an electron transition from a higher energy (E subscript 2) to a lower energy level (E subscript 1). The transition results in a photon of energy E subscript 2 minus E subscript 1 being released. The frequency of the photon is proportional to its energy.
Question 10
10. Before assigning a new chapter in the textbook, a physics teacher regularly walks students through the chapter's headings, subheadings, and objectives. The teacher also encourages the students to read the chapter's introduction and summary before they read the entire chapter. These practices promote comprehension of a content-area text most directly by helping the students:
- determine what is most important to learn from their reading.
- match new vocabulary words in the text to the words' definitions.
- identify supplemental materials that are relevant to their reading.
- analyze the text from multiple viewpoints and perspectives.
Answer to question 10
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: A. (Objective 0003) A chapter's headings, subheadings, objectives, introductions, and summaries provide a clear indication of the chapter's main ideas in a concise format. When previewed before reading, these textual features provide students with guidance regarding what information in the chapter is most important, which can help them set a purpose, or personal learning goals, for their reading.
Correct Response: A. (Objective 0003) A chapter's headings, subheadings, objectives, introductions, and summaries provide a clear indication of the chapter's main ideas in a concise format. When previewed before reading, these textual features provide students with guidance regarding what information in the chapter is most important, which can help them set a purpose, or personal learning goals, for their reading.
Question 11
11. Some students in a physics class are having difficulty understanding the textbook and other reading assignments even though they demonstrate sufficient background knowledge during prereading discussions and their school records indicate that they have adequate basic reading skills. These students would likely benefit most from differentiated content-area reading instruction focused on promoting their ability to use:
- decoding strategies such as orthographic, syllabic, and structural analysis.
- textual features such as subject indexes and glossaries.
- self-monitoring strategies such as questioning, mental imagery, and rereading.
- online research tools such as search engines and databases.
Answer to question 11
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0003) Background knowledge includes foundational concepts and information and vocabulary related to a specific topic. Since the students who are having difficulty demonstrate the background knowledge necessary to comprehend the reading assignments as well as the basic reading skills to decode the assignments, the source of their comprehension difficulty must be in recognizing the purpose and organizational structures in the passages, in constructing meaning as they read, or in both. Self-monitoring strategies such as questioning, mental imagery, and rereading promote comprehension by supporting active engagement with the meaning of the text, metacognitive awareness of gaps in comprehension, and the use of strategies to repair comprehension during reading.
Correct Response: C. (Objective 0003) Background knowledge includes foundational concepts and information and vocabulary related to a specific topic. Since the students who are having difficulty demonstrate the background knowledge necessary to comprehend the reading assignments as well as the basic reading skills to decode the assignments, the source of their comprehension difficulty must be in recognizing the purpose and organizational structures in the passages, in constructing meaning as they read, or in both. Self-monitoring strategies such as questioning, mental imagery, and rereading promote comprehension by supporting active engagement with the meaning of the text, metacognitive awareness of gaps in comprehension, and the use of strategies to repair comprehension during reading.
Question 12
12. A physics teacher regularly uses close reading and think-alouds with complex informational texts to model and provide students with guided practice deconstructing syntactically complex sentences (e.g., passive-voice constructions, multiple clauses) and using various word-learning strategies to deduce the meaning of unfamiliar academic vocabulary encountered in the text. The teacher's practices are likely to support struggling readers in the class primarily by:
- promoting the students' interest in and motivation to read complex academic texts independently.
- addressing gaps in the students' background knowledge related to the text's content.
- teaching the students strategies for resolving common reading comprehension problems.
- improving the students' print processing abilities with respect to their decoding skills.
Answer to question 12
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0003) Research indicates that reading is essential for academic language development and that struggling readers fall increasingly behind their peers in academic language knowledge during the elementary school years and beyond because they tend to read less than their peers. Lack of academic language knowledge is a common contributing factor to comprehension difficulties for students beyond the primary grades. Even students who have strong decoding skills but limited academic language knowledge experience comprehension difficulties when reading complex academic texts. Providing students with instruction that helps them deconstruct complex sentence structures and determine the meaning of unfamiliar words in context promotes their ability to construct meaning from complex content-area texts.
Correct Response: C. (Objective 0003) Research indicates that reading is essential for academic language development and that struggling readers fall increasingly behind their peers in academic language knowledge during the elementary school years and beyond because they tend to read less than their peers. Lack of academic language knowledge is a common contributing factor to comprehension difficulties for students beyond the primary grades. Even students who have strong decoding skills but limited academic language knowledge experience comprehension difficulties when reading complex academic texts. Providing students with instruction that helps them deconstruct complex sentence structures and determine the meaning of unfamiliar words in context promotes their ability to construct meaning from complex content-area texts.
Question 13
13. A physics teacher notices that many students forget or begin confusing new discipline-specific vocabulary shortly after an assessment. Which of the following instructional strategies would be most effective in promoting the students' understanding and retention of new vocabulary that has been explicitly taught?
- teaching the students how to use independent word-learning strategies to determine the meaning of unfamiliar vocabulary
- providing the students with repeated exposure to and opportunities to use new vocabulary in context
- promoting the students' recognition of discipline-specific language structures and functions
- improving the students' word-identification skills and oral reading fluency using grade-level content-area word lists
Answer to question 13
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0003) Vocabulary knowledge and concept development are closely interrelated; discipline-specific vocabulary development involves concept learning, and concept learning supports academic vocabulary development. Vocabulary development is an incremental process; more exposures to and opportunities to use new vocabulary in conceptually meaningful contexts result in greater depth of understanding and improved retention.
Correct Response: B. (Objective 0003) Vocabulary knowledge and concept development are closely interrelated; discipline-specific vocabulary development involves concept learning, and concept learning supports academic vocabulary development. Vocabulary development is an incremental process; more exposures to and opportunities to use new vocabulary in conceptually meaningful contexts result in greater depth of understanding and improved retention.
Question 14
14. The graph below represents the velocity versus time of an object moving in one dimension along the x-axis. At t = 0.0
s, the position of the object is x = 32
m.
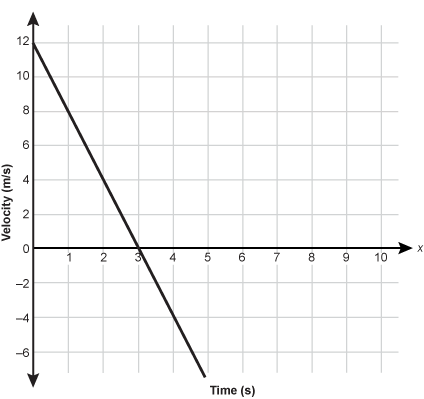
Start line starting at open parenthesis zero comma twelve and decreasing steadily passing through open parenthesis two comma four close parenthesis and passing the x axis at three into the fourth quadrant continuing to decrease through open parenthesis four comma negative four close parenthesis
Which of the following best describes the motion of the object?
- Its acceleration is zero at t = 0
s.
- It is located at the origin at t = 3
s.
- It is moving in the negative x-direction at t = 4
s.
- Its distance from the origin is maximum at t = 0
s.
Answer to question 14
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0004) The graph shows the velocity of an object moving in one dimension. According to the graph, at t = 0.0 s, the object is moving to the right along the x-axis at 12 m/s and slowing down at a constant rate. At t = 3 s the object has momentarily stopped moving and has a velocity of 0 m/s. When t > 3 s, the object's velocity is negative, meaning it has changed direction and is moving in the negative x-direction.
Correct Response: C. (Objective 0004) The graph shows the velocity of an object moving in one dimension. According to the graph, at t equals 0.0 seconds, the object is moving to the right along the x-axis at 12 meters per second and slowing down at a constant rate. At t equals 3 seconds the object has momentarily stopped moving and has a velocity of 0 meters per second. When t greater then 3 seconds, the object's velocity is negative, meaning it has changed direction and is moving in the negative x-direction.
Question 15
15. A satellite orbits the earth in a circular path once per day at a constant speed and at a distance of 42,164 × times 103
m
from the center of the earth. Which of the following expressions equals the acceleration of the satellite?
-
 start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four close parenthesis open parenthesis sixty close parenthesis end fraction m/s2meters per second squared
start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four close parenthesis open parenthesis sixty close parenthesis end fraction m/s2meters per second squared
-
 start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four open parenthesis sixty close parenthesis squared close parenthesis end fraction m/s2meters per second squared
start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four open parenthesis sixty close parenthesis squared close parenthesis end fraction m/s2meters per second squared
-
 start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four open parenthesis sixty close parenthesis close parenthesis squared m/s2meters per second squared
start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four open parenthesis sixty close parenthesis close parenthesis squared m/s2meters per second squared
-
 start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four open parenthesis sixty close parenthesis squared close parenthesis m/s2meters per second squared
start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four open parenthesis sixty close parenthesis squared close parenthesis m/s2meters per second squared
Answer to question 15
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: D. (Objective 0004) The satellite is an example of an object undergoing uniform circular motion. The acceleration vector always points toward the center of the circular path taken by the object and the magnitude is given by
 .
Let T be the period of the satellite's orbit and R its radius. Then the speed of the satellite is given by the circumference of the orbit divided by the time required to complete the orbit, T, so
.
Let T be the period of the satellite's orbit and R its radius. Then the speed of the satellite is given by the circumference of the orbit divided by the time required to complete the orbit, T, so
 . Thus,
. Thus,
 .
Substituting the values given and converting 24 hours to seconds gives
.
Substituting the values given and converting 24 hours to seconds gives
 m/s2.
Correct Response: D. (Objective 0004) The satellite is an example of an object undergoing uniform circular motion. The acceleration vector always points toward the center of the circular path taken by the object and the magnitude is given by a equals start fraction numerator v squared denominator r end fraction. Let T be the period of the satellite's orbit and R its radius. Then the speed of the satellite is given by the circumference of the orbit divided by the time required to complete the orbit, T, so v equals start fraction numerator two pi r denominator t end fraction. Thus, a equals start fraction numerator v squared denominator r end fraction equals start fraction numerator open parenthesis two pi upper r close parenthesis squared denominator t squared end fraction divided by upper r equals start fraction numerator four pi squared upper r denominator t squared end fraction. Substituting the values given and converting 24 hours to seconds gives start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four open parenthesis sixty close parenthesis squared close parenthesis squared end fraction meters per second squared.
m/s2.
Correct Response: D. (Objective 0004) The satellite is an example of an object undergoing uniform circular motion. The acceleration vector always points toward the center of the circular path taken by the object and the magnitude is given by a equals start fraction numerator v squared denominator r end fraction. Let T be the period of the satellite's orbit and R its radius. Then the speed of the satellite is given by the circumference of the orbit divided by the time required to complete the orbit, T, so v equals start fraction numerator two pi r denominator t end fraction. Thus, a equals start fraction numerator v squared denominator r end fraction equals start fraction numerator open parenthesis two pi upper r close parenthesis squared denominator t squared end fraction divided by upper r equals start fraction numerator four pi squared upper r denominator t squared end fraction. Substituting the values given and converting 24 hours to seconds gives start fraction numerator open parenthesis four pi squared close parenthesis open parenthesis forty two thousand one hundred and sixty four times ten cubed close parenthesis denominator open parenthesis twenty four open parenthesis sixty close parenthesis squared close parenthesis squared end fraction meters per second squared.
Question 16
16. The graph below shows the angular speed, in
rad/s, of the central shaft of a wind turbine as a function of time. At t = 0.0
s, the angular displacement of the shaft is π
rad.
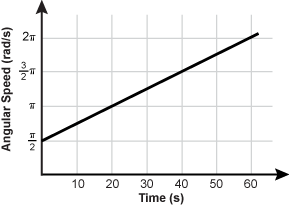
graph showing angular speed in radians per second on the y axis and time in seconds on the x axis. the straight line starts at open parenthesis zero comma pi over two close parenthesis and increases in a steady fashion passing through open parenthesis twenty comma pi close parenthesis then through open parenthesis forty comma three halves pi close parenthesis and continuing to increase as time goes on
Which of the following equations gives the angular displacement of the shaft in radians with respect to time in seconds?
-
 theta of t equals pi over eighty baseline t squared plus pi t
theta of t equals pi over eighty baseline t squared plus pi t
-
 theta of t equals pi over eighty baseline t squared plus pi over two baseline t plus pi
theta of t equals pi over eighty baseline t squared plus pi over two baseline t plus pi
-
 theta of t equals pi over forty baseline t squared plus pi t plus pi
theta of t equals pi over forty baseline t squared plus pi t plus pi
-
 theta of t equals pi over forty baseline t squared plus pi over two t plus pi
theta of t equals pi over forty baseline t squared plus pi over two t plus pi
Answer to question 16
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0004) The graph gives the angular speed of the shaft with respect to time. According to the graph, at t = 0.0 s, the angular speed is
 rad/s. The angular acceleration is constant and equal to the slope of the line, which is
rad/s. The angular acceleration is constant and equal to the slope of the line, which is

 rad/s2. Since the acceleration is constant, the equations of motion for constant acceleration can be used. The angular displacement for an object undergoing constant angular acceleration is given by
rad/s2. Since the acceleration is constant, the equations of motion for constant acceleration can be used. The angular displacement for an object undergoing constant angular acceleration is given by
 , where α = the angular acceleration, ω0 = the initial angular speed, and θ0 = the initial angular displacement. Using these values, and given that θ0 = π rad, one obtains
, where α = the angular acceleration, ω0 = the initial angular speed, and θ0 = the initial angular displacement. Using these values, and given that θ0 = π rad, one obtains
 .
Correct Response: B. (Objective 0004) The graph gives the angular speed of the shaft with respect to time. According to the graph, at t equals 0.0 s, the angular speed is pi over two radians per second. The angular acceleration is constant and equal to the slope of the line, which is alpha equals delta omega over delta t equals start fraction omega subscript two baseline minus omega subscript one denominator t subscript two baseline minus t subscript one end fraction equals start fraction numerator two pi radians per second minus open parenthesis pi over two radians per second close parenthesis denominator sixty seconds minus zero seconds end fraction equals start fraction numerator three halves pi radians per second denominator sixty seconds end fraction equals pi over forty radians per second squared. Since the acceleration is constant, the equations of motion for constant acceleration can be used. The angular displacement for an object undergoing constant angular acceleration is given by theta of t equals one half alpha t squared plus omega subscript zero baseline t plus theta subscript zero, where alpha equals the angular acceleration, omega subscript zero equals the initial angular speed, and theta subscript zero equals the initial angular displacement. Using these values, and given that omega subscript zero equals pi radian, one obtains theta of t equals pi over eighty baseline t squared plus pi over two baseline t plus pi.
.
Correct Response: B. (Objective 0004) The graph gives the angular speed of the shaft with respect to time. According to the graph, at t equals 0.0 s, the angular speed is pi over two radians per second. The angular acceleration is constant and equal to the slope of the line, which is alpha equals delta omega over delta t equals start fraction omega subscript two baseline minus omega subscript one denominator t subscript two baseline minus t subscript one end fraction equals start fraction numerator two pi radians per second minus open parenthesis pi over two radians per second close parenthesis denominator sixty seconds minus zero seconds end fraction equals start fraction numerator three halves pi radians per second denominator sixty seconds end fraction equals pi over forty radians per second squared. Since the acceleration is constant, the equations of motion for constant acceleration can be used. The angular displacement for an object undergoing constant angular acceleration is given by theta of t equals one half alpha t squared plus omega subscript zero baseline t plus theta subscript zero, where alpha equals the angular acceleration, omega subscript zero equals the initial angular speed, and theta subscript zero equals the initial angular displacement. Using these values, and given that omega subscript zero equals pi radian, one obtains theta of t equals pi over eighty baseline t squared plus pi over two baseline t plus pi.
Question 17
17. A marble rolls across a horizontal table with a velocity of 25
cm/second. When it reaches the edge of the table, it falls a distance d of 0.85
m
to the floor below. At what horizontal distance from the edge of the table does the marble land on the floor?
- 0.07
m
- 0.11
m
- 0.75
m
- 1.0
m
Answer to question 17
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0004) The distance the marble travels in the horizontal direction in any time interval is equal to the x-component of velocity multiplied by the time interval d = vx • t. The time for the marble to drop from the top of the table to the floor is independent of the x-component of velocity and is the same as the amount of time for an object at rest to fall the same distance. It can be found by
 where h represents the height of the table and g is the acceleration due to gravity, or 9.8 m/s2. Solving for time gives t = 0.42 s. The horizontal distance the marble travels while falling from the top of the table to the floor is d = (0.25 m/s) (0.42 s) = 0.11 m.
Correct Response: B. (Objective 0004) The distance the marble travels in the horizontal direction in any time interval is equal to the x-component of velocity multiplied by the time interval d equals v subscript x times t. The time for the marble to drop from the top of the table to the floor is independent of the x-component of velocity and is the same as the amount of time for an object at rest to fall the same distance. It can be found by t equals the square root of the quantity 2h over g where h represents the height of the table and g is the acceleration due to gravity, or 9.8 meters per second squared. Solving for time gives t equals 0.42 seconds. The horizontal distance the marble travels while falling from the top of the table to the floor is d equals (0.25 meters per second) (0.42 second) equals 0.11 meter.
where h represents the height of the table and g is the acceleration due to gravity, or 9.8 m/s2. Solving for time gives t = 0.42 s. The horizontal distance the marble travels while falling from the top of the table to the floor is d = (0.25 m/s) (0.42 s) = 0.11 m.
Correct Response: B. (Objective 0004) The distance the marble travels in the horizontal direction in any time interval is equal to the x-component of velocity multiplied by the time interval d equals v subscript x times t. The time for the marble to drop from the top of the table to the floor is independent of the x-component of velocity and is the same as the amount of time for an object at rest to fall the same distance. It can be found by t equals the square root of the quantity 2h over g where h represents the height of the table and g is the acceleration due to gravity, or 9.8 meters per second squared. Solving for time gives t equals 0.42 seconds. The horizontal distance the marble travels while falling from the top of the table to the floor is d equals (0.25 meters per second) (0.42 second) equals 0.11 meter.
Question 18
18. A wooden block is given an initial push and slides across a rough horizontal surface with an acceleration of –negative a. The block then slides down a plane inclined at an angle θtheta as shown in the diagram below.
 The line then slopes downward to the right, forming an inclined plane. The angle that the incline makes with the horizontal is theta. A shaded rectangular box is drawn on the horizontal section. An arrow labeled v points to the right, in the direction of the incline. An arrow labeled a points to the left.
The line then slopes downward to the right, forming an inclined plane. The angle that the incline makes with the horizontal is theta. A shaded rectangular box is drawn on the horizontal section. An arrow labeled v points to the right, in the direction of the incline. An arrow labeled a points to the left.
If the coefficient of friction has the same value on the horizontal plane and the inclined plane, what is the magnitude of the acceleration of the block down the plane?
- | –a + g sin θ | the absolute value of the quantity negative a plus g sine of theta
- | –a sin θ + g sin θ | the absolute value of the quantity negative a sine of theta plus g sine of theta
- | –a sin θ + g cos θ | the absolute value of the quantity negative a sine of theta plus g cosine of theta
- | –a cos θ + g sin θ | the absolute value of the quantity negative a cosine of theta plus g sine of theta
Answer to question 18
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: D. (Objective 0005) The diagram below shows free-body diagrams for the block sliding on the horizontal surface and for the block sliding down the inclined plane.
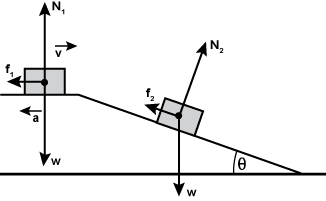
Applying Newton's second law for the block sliding on the horizontal surface gives N1 = W = mg for the direction perpendicular to the horizontal surface and f1 = ma for the direction parallel to the horizontal surface. Then using f1 = μN1 these equations give a = μg. Applying Newton's second law for the block sliding down the inclined plane gives N2 = W cos θ = mg cos θ for the direction perpendicular to the inclined plane. For the direction parallel to the inclined plane, we'll choose the +x direction to be down the plane. Then Newton's second law gives –f2 + mg sin θ = ma2, where a2 is the acceleration down the plane. Then using f2 = μN2 these equations give a2 = –μg cos θ + g sin θ = –a cos θ + g sin θ. The magnitude of the acceleration as the block slides down the inclined plane is | –a cos θ + g sin θ |.
Correct Response: D. (Objective 0005) The diagram below shows free-body diagrams for the block sliding on the horizontal surface and for the block sliding down the inclined plane. The diagram shows an inclined plane with angle theta. The top of the plane is a horizontal surface. On the horizontal surface, a free body diagram shows the following vectors acting on a rectangular object. f subscript 1 points to the left, N subscript 1 points up in the positive vertical direction and w points down in the negative vertical direction. On the inclined surface, the rectangular object is redrawn and has the following vectors. f subscript 2 is pointing up the inclined plane, N subscript 2 is pointing upwards perpendicular to the inclined surface, and W is pointing straight down in the negative vertical direction. Applying Newton's second law for the block sliding on the horizontal surface gives N subscript 1 = W = mg for the direction perpendicular to the horizontal surface and f subscript 1 = m a for the direction parallel to the horizontal surface. Then using f subscript 1 = mu N subscript 1 these equations give a = mu g. Applying Newton's second law for the block sliding down the inclined plane gives N subscript 2 = W cosine theta = mg cosine theta for the direction perpendicular to the inclined plane. For the direction parallel to the inclined plane, we'll choose the positive x direction to be down the plane. Then Newton's second law gives negative f subscript 2 + mg sine theta = m a subscript 2, where a subscript 2 is the acceleration down the plane. Then using f subscript 2 = mu N subscript 2 these equations give a subscript 2 = negative mu g cosine theta + g sine theta = negative a cosine theta + g sine theta. The magnitude of the acceleration as the block slides down the inclined plane is the absolute value of negative a cosine theta + g sine theta.
Question 19
19. A 50
kg
person stands on a scale in an elevator. The graph below shows the velocity of the elevator moving upward in the positive y-direction.
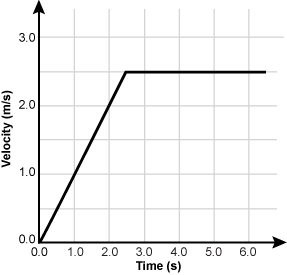
graph showing velocity in meters per second on the y axis and time in seconds on the x axis. starting at the origin increasing at a steady rate passing through open parenthesis one point zero comma one point zero close parenthesis and open parenthesis two point zero comma two point zero close parenthesis until it stops increasing and stays constant at around open parenthesis two point four comma two point five close parenthesis. The line continues to stay constant as time goes on past six seconds.
What does the scale read at t = 2.0 s?
- 440
N
- 490
N
- 540
N
- 590
N
Answer to question 19
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0005) The acceleration of the elevator, a, at t = 2.0 s points in the positive y-direction. According to the graph, the magnitude of the acceleration is given by the slope of the velocity-versus-time curve at t = 2.0 s, which is 1.0 m/s2. The forces acting on the person standing in the elevator are the force of gravity, mg, in the negative y-direction and the normal force of the scale on the person, N, in the positive y-direction. Newton's second law states that
 . Since all of the forces act in the y-direction,
. Since all of the forces act in the y-direction,  . The scale exerts a normal force on the person, and according to Newton's third law, the person exerts a force on the scale equal in magnitude and opposite in direction to the normal force, N. The scale reads the magnitude of this equal and opposite force, which is equal to N. Solving the equation ma = N − mg for N gives N = ma + mg and substituting the values from above results in N = (50 kg)(1.0 m/s2) + (50 kg)(9.8 m/s2) = 540 N.
Correct Response: C. (Objective 0005) The acceleration of the elevator, a, at t equals 2.0 s points in the positive y direction. According to the graph, the magnitude of the acceleration is given by the slope of the velocity-versus-time curve at t equals 2.0 s, which is 1.0 m slash s squared. The forces acting on the person standing in the elevator are the force of gravity, m g, in the negative y direction and the normal force of the scale on the person, N, in the positive y direction. Newton's second law states that sigma summation of f equals m a. Since all of the forces act in the y direction, sigma summation of f equals m a equals n minus m g. The scale exerts a normal force on the person, and according to Newton's third law, the person exerts a force on the scale equal in magnitude and opposite in direction to the normal force, N. The scale reads the magnitude of this equal and opposite force, which is equal to N. Solving the equation m a equals N minus m g for N gives N equals m a plus m g and substituting the values from above results in N equals open parenthesis 50 kilograms close parenthesis times open parenthesis 1.0 meter per second squared close parenthesis plus open parenthesis 50 kilograms close parenthesis open parenthesis 9.8 meter per second squared close parenthesis equals 540 Newtons.
. The scale exerts a normal force on the person, and according to Newton's third law, the person exerts a force on the scale equal in magnitude and opposite in direction to the normal force, N. The scale reads the magnitude of this equal and opposite force, which is equal to N. Solving the equation ma = N − mg for N gives N = ma + mg and substituting the values from above results in N = (50 kg)(1.0 m/s2) + (50 kg)(9.8 m/s2) = 540 N.
Correct Response: C. (Objective 0005) The acceleration of the elevator, a, at t equals 2.0 s points in the positive y direction. According to the graph, the magnitude of the acceleration is given by the slope of the velocity-versus-time curve at t equals 2.0 s, which is 1.0 m slash s squared. The forces acting on the person standing in the elevator are the force of gravity, m g, in the negative y direction and the normal force of the scale on the person, N, in the positive y direction. Newton's second law states that sigma summation of f equals m a. Since all of the forces act in the y direction, sigma summation of f equals m a equals n minus m g. The scale exerts a normal force on the person, and according to Newton's third law, the person exerts a force on the scale equal in magnitude and opposite in direction to the normal force, N. The scale reads the magnitude of this equal and opposite force, which is equal to N. Solving the equation m a equals N minus m g for N gives N equals m a plus m g and substituting the values from above results in N equals open parenthesis 50 kilograms close parenthesis times open parenthesis 1.0 meter per second squared close parenthesis plus open parenthesis 50 kilograms close parenthesis open parenthesis 9.8 meter per second squared close parenthesis equals 540 Newtons.
Question 20
20. A 6.0
kg
box is pulled across a rough floor by a rope attached to the box as shown in the diagram below.
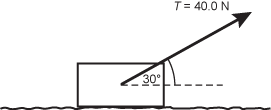
A rope is connected to the center of the box and is thirty degrees off the horizontal. T equals forty point zero N for the rope.
The tension in the rope is 40.0
N. If the coefficient of friction between the floor and the box is 0.3, what is the magnitude of the frictional force on the box?
- 6.0
N
- 12
N
- 18
N
- 24
N
Answer to question 20
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0005) The forces on the box in the x-direction are the component of the rope acting to the right (T cos θ ) and the frictional force (f) acting to the left. The sum of the forces in the x-direction can be written as
 . Since the x-acceleration is unknown, the frictional force cannot be found from this equation. The forces acting on the mass in the y-direction are the normal force from the ground on the box (N) acting upward, gravity (mg) acting downward, and the component of the rope (T sin θ) acting upward. The sum of the forces in the y-direction can be written as
. Since the x-acceleration is unknown, the frictional force cannot be found from this equation. The forces acting on the mass in the y-direction are the normal force from the ground on the box (N) acting upward, gravity (mg) acting downward, and the component of the rope (T sin θ) acting upward. The sum of the forces in the y-direction can be written as
 . Because the object is not accelerating in the y-direction, ay = 0 and the equation becomes 0 = T sin θ + N – mg. The magnitude of the frictional force is given by f = μ N. Solving the above equation for the normal force and substituting it into the equation for the frictional force gives f = μ (mg – T sin θ ) = (0.3)[(6.0 kg)(9.8 m/s2) – 0.5(40 N)] = 11.6 N = 12 N.
Correct Response: B. (Objective 0005) The forces on the box in the x direction are the component of the rope acting to the right open parenthesis T cosine theta close parenthesis and the frictional force open parenthesis f close parenthesis acting to the left. The sum of the forces in the x direction can be written as sigma summation of F subscript x baseline equals m a subscript x baseline equals T cosine theta plus f. Since the x acceleration is unknown, the frictional force cannot be found from this equation. The forces acting on the mass in the y direction are the normal force from the ground on the box (N) acting upward, gravity (mg) acting downward, and the component of the rope (T sine theta) acting upward. The sum of the forces in the y direction can be written as sigma summation of f subscript y baseline equals m a subscript y baseline equals t sine theta plus n minus m g. Because the object is not accelerating in the y direction, a subscript y equals 0 and the equation becomes 0 equals T sine theta plus N minus m g. The magnitude of the frictional force is given by f equals mu N. Solving the above equation for the normal force and substituting it into the equation for the frictional force gives f equals mu open parenthesis m g minus T sine theta close parenthesis equals open parenthesis 0.3 close parenthesis left bracket open parenthesis 6.0 kilograms close parenthesis open parenthesis 9.8 meters per second squared close minus 0.5 open parenthesis 40 Newtons close parenthesis right bracket equals 11.6 Newtons equals 12 Newtons.
. Because the object is not accelerating in the y-direction, ay = 0 and the equation becomes 0 = T sin θ + N – mg. The magnitude of the frictional force is given by f = μ N. Solving the above equation for the normal force and substituting it into the equation for the frictional force gives f = μ (mg – T sin θ ) = (0.3)[(6.0 kg)(9.8 m/s2) – 0.5(40 N)] = 11.6 N = 12 N.
Correct Response: B. (Objective 0005) The forces on the box in the x direction are the component of the rope acting to the right open parenthesis T cosine theta close parenthesis and the frictional force open parenthesis f close parenthesis acting to the left. The sum of the forces in the x direction can be written as sigma summation of F subscript x baseline equals m a subscript x baseline equals T cosine theta plus f. Since the x acceleration is unknown, the frictional force cannot be found from this equation. The forces acting on the mass in the y direction are the normal force from the ground on the box (N) acting upward, gravity (mg) acting downward, and the component of the rope (T sine theta) acting upward. The sum of the forces in the y direction can be written as sigma summation of f subscript y baseline equals m a subscript y baseline equals t sine theta plus n minus m g. Because the object is not accelerating in the y direction, a subscript y equals 0 and the equation becomes 0 equals T sine theta plus N minus m g. The magnitude of the frictional force is given by f equals mu N. Solving the above equation for the normal force and substituting it into the equation for the frictional force gives f equals mu open parenthesis m g minus T sine theta close parenthesis equals open parenthesis 0.3 close parenthesis left bracket open parenthesis 6.0 kilograms close parenthesis open parenthesis 9.8 meters per second squared close minus 0.5 open parenthesis 40 Newtons close parenthesis right bracket equals 11.6 Newtons equals 12 Newtons.
Question 21
21. A mass m is attached to the end of a very light pole of length L. One end of the pole is connected by a hinge to a wall and the other end is secured by a rope attached to the wall, as shown in the diagram below.
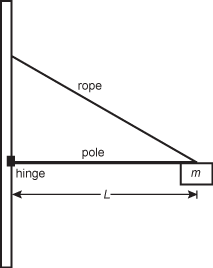
Where the mass and the pole meet there is also a rope attached that leads back to the wall some distance up from where the pole attaches to the wall
Suddenly, the rope breaks. What is the angular acceleration of the pole with respect to the hinge the instant the rope breaks?
-
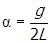
-
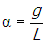
-

-

Answer to question 21
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0005) Newton's second law for rotational systems is
 . When the rope breaks, there will be a torque due to the weight of the mass and the pole will begin to rotate clockwise around the hinge. This torque will not be constant, because as the pole rotates, the lever arm (the perpendicular distance from the force to the point of rotation) of the force changes. However, the instant the rope breaks, the force is perpendicular to the lever arm and the magnitude of the torque is given by Fr, where F = mg is the force and r = L is the lever arm. The moment of inertia of an object depends on how the mass is distributed with respect to its rotational axis. For a discrete mass distribution it is given by
. When the rope breaks, there will be a torque due to the weight of the mass and the pole will begin to rotate clockwise around the hinge. This torque will not be constant, because as the pole rotates, the lever arm (the perpendicular distance from the force to the point of rotation) of the force changes. However, the instant the rope breaks, the force is perpendicular to the lever arm and the magnitude of the torque is given by Fr, where F = mg is the force and r = L is the lever arm. The moment of inertia of an object depends on how the mass is distributed with respect to its rotational axis. For a discrete mass distribution it is given by
 . Since the mass is located a distance L from the hinge, the moment of inertia of the pole/mass system is mL2. Newton's second law becomes mL2α = mgL and
. Since the mass is located a distance L from the hinge, the moment of inertia of the pole/mass system is mL2. Newton's second law becomes mL2α = mgL and
 .
Correct Response: B. (Objective 0005) Newton's second law for rotational systems is sigma summation of tau equals iota alpha. When the rope breaks, there will be a torque due to the weight of the mass and the pole will begin to rotate clockwise around the hinge. This torque will not be constant, because as the pole rotates, the lever arm (the perpendicular distance from the force to the point of rotation) of the force changes. However, the instant the rope breaks, the force is perpendicular to the lever arm and the magnitude of the torque is given by F r, where F equals m g is the force and r equals L is the lever arm. The moment of inertia of an object depends on how the mass is distributed with respect to its rotational axis. For a discrete mass distribution it is given by Iota equals sigma summation underscript baseline m subscript i r subscript i baseline squared. Since the mass is located a distance L from the hinge, the moment of inertia of the pole slash mass system is m L squared. Newton's second law becomes m L squared alpha equals m g L and alpha equals g over l.
.
Correct Response: B. (Objective 0005) Newton's second law for rotational systems is sigma summation of tau equals iota alpha. When the rope breaks, there will be a torque due to the weight of the mass and the pole will begin to rotate clockwise around the hinge. This torque will not be constant, because as the pole rotates, the lever arm (the perpendicular distance from the force to the point of rotation) of the force changes. However, the instant the rope breaks, the force is perpendicular to the lever arm and the magnitude of the torque is given by F r, where F equals m g is the force and r equals L is the lever arm. The moment of inertia of an object depends on how the mass is distributed with respect to its rotational axis. For a discrete mass distribution it is given by Iota equals sigma summation underscript baseline m subscript i r subscript i baseline squared. Since the mass is located a distance L from the hinge, the moment of inertia of the pole slash mass system is m L squared. Newton's second law becomes m L squared alpha equals m g L and alpha equals g over l.
Question 22
22. A physics teacher is using a drone aircraft to demonstrate the forces acting on a craft in flight. Which of the following relationships would be used to label a free-body diagram illustrating the motion of the drone at a constant horizontal velocity and upward acceleration?
- Thrust = Drag; Lift = Weight
- Thrust < is less than Drag; Lift = Weight
- Thrust = Drag; Lift > is greater than Weight
- Thrust > is greater than Drag; Lift > is greater than Weight
Answer to question 22
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0005) The four forces acting on a vehicle in flight are thrust and drag in the horizontal direction, and lift and weight in the vertical direction. The drone is moving with a constant horizontal velocity, so the net horizontal force equals zero, therefore Thrust = Drag. If the lift force and weight were the same, the object would remain stationary in height above some reference point. Since the object is accelerating upward, there must be a net upward force, so Lift > Weight.
Correct Response: C. (Objective 0005) The four forces acting on a vehicle in flight are thrust and drag in the horizontal direction, and lift and weight in the vertical direction. The drone is moving with a constant horizontal velocity, so the net horizontal force equals zero, therefore Thrust = Drag. If the lift force and weight were the same, the object would remain stationary in height above some reference point. Since the object is accelerating upward, there must be a net upward force, so Lift is greater than Weight.
Question 23
23. A 40.0 kg mass on a 4.00 m long rope swing starts to swing from rest at a height of 2.00 m above the equilibrium position of the swing, as shown in the diagram below. Initially, the angle made by the rope is 60.0° with the vertical.

What is the magnitude of the tension in the rope when the mass passes through the equilibrium position for the first time?
23. A forty point zero kilogram mass on a four point zero-zero meters long rope swing starts to swing from rest at a height of two point zero-zero meters above the equilibrium position of the swing, as shown in the diagram below. Initially, the angle made by the rope is sixty point zero degrees with the vertical. The swing is represented as a ball attached to a rope. The situation resembles a pendulum bob pulled to the left. The ball is two meters above its equilibrium position. A dotted vertical line goes from the top of the swing to the equilibrium position of the swing. The angle between the displaced swing and the vertical line is sixty degrees. The distance from the equilibrium position to the top of the swing is 4 meters. What is the magnitude of the tension in the rope when the mass passes through the equilibrium position for the first time?
- 392 N newtons
- 784 N newtons
- 1176 N newtons
- 1568 N newtons
Answer to question 23
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0006) When the mass is at the equilibrium position, the force due to the tension is directed up, the weight force is directed down, and the acceleration of the mass is a centripetal acceleration directed up toward the center of the circular path of the mass. Newton's second law gives T − mg = ma. Then using the formula for the centripetal acceleration, T = mg + mv2/R. To find the speed of the mass, apply the principle of conservation of mechanical energy. At the top of the swing the mass has no kinetic energy. At the equilibrium position the mass has kinetic energy but no gravitational potential energy if we take this point to be the zero point of gravitational potential energy. With this choice, the mass has gravitational potential energy of mgh at the top of the swing. So
 and v2 = 2gh. So T = mg [1 + (2h/R)]. Substituting the data into the equation gives the desired result.
Correct Response: B. (Objective 0006) When the mass is at the equilibrium position, the force due to the tension is directed up, the weight force is directed down, and the acceleration of the mass is a centripetal acceleration directed up toward the center of the circular path of the mass. Newton's second law gives T − mg = m a. Then using the formula for the centripetal acceleration, T = mg + mv squared over R. To find the speed of the mass, apply the principle of conservation of mechanical energy. At the top of the swing the mass has no kinetic energy. At the equilibrium position the mass has kinetic energy but no gravitational potential energy if we take this point to be the zero point of gravitational potential energy. With this choice, the mass has gravitational potential energy of mgh at the top of the swing. So mgh = one half m v squared and v squared = 2gh. So T = mg times the quantity 1 + 2h over R. Substituting the data into the equation gives the desired result.
and v2 = 2gh. So T = mg [1 + (2h/R)]. Substituting the data into the equation gives the desired result.
Correct Response: B. (Objective 0006) When the mass is at the equilibrium position, the force due to the tension is directed up, the weight force is directed down, and the acceleration of the mass is a centripetal acceleration directed up toward the center of the circular path of the mass. Newton's second law gives T − mg = m a. Then using the formula for the centripetal acceleration, T = mg + mv squared over R. To find the speed of the mass, apply the principle of conservation of mechanical energy. At the top of the swing the mass has no kinetic energy. At the equilibrium position the mass has kinetic energy but no gravitational potential energy if we take this point to be the zero point of gravitational potential energy. With this choice, the mass has gravitational potential energy of mgh at the top of the swing. So mgh = one half m v squared and v squared = 2gh. So T = mg times the quantity 1 + 2h over R. Substituting the data into the equation gives the desired result.
Question 24
24. The diagram below shows the potential energy of a 6.0
kg
mass with respect to position. The only force on the object is a conservative force.
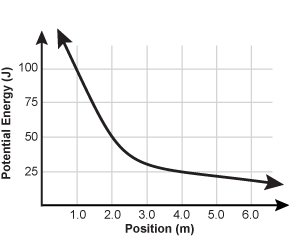
graph showing the potential energy in joules on the y axis and position in meters on the x axis starting high above one hundred joules near the y axis and less then one meter passing through open parenthesis one point zero comma one hundred and decreasing quickly until about open parenthesis two point zero comma fifty close parenthesis where the decrease slows pretty dramatically passing through open parenthesis four point zero comma twenty five close parenthesis and continuing to decrease almost horizontally as it is approaching the x axis
If the particle is released from rest at x = 1.0
meters, what is the speed of the particle at x = 4.0
meters?
- 2.9
m/s
- 4.0
m/s
- 5.0
m/s
- 5.7
m/s
Answer to question 24
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0006) At em>x = 1.0 m, the potential energy of the particle is 100 J. Since the particle is at rest, this is equal to its total energy. At x = 4.0 m, the potential energy of the particle is 25 J, so the change in energy of the particle is Δ E = 25 J – 100 J = –75 J. Because there are no other forces acting, the total energy is conserved and the change in the total energy is zero: Δ E = Δ K + Δ U = 0. This gives the change in kinetic energy of the particle, Δ K = –Δ U = 75 J. The change in the kinetic energy of the particle is
 . Since the initial kinetic energy of the particle equals 0.0 J,
. Since the initial kinetic energy of the particle equals 0.0 J,
 . Solving this equation using the given values and solving for the speed, v, results in v = 5.0 m/s.
Correct Response: C. (Objective 0006) At x equals 1.0 m, the potential energy of the particle is 100 J. Since the particle is at rest, this is equal to its total energy. At x equals 4.0 m, the potential energy of the particle is 25 Joules, so the change in energy of the particle is delta E equals 25 Joules minus 100 Joules equals negative 75 Joules. Because there are no other forces acting, the total energy is conserved and the change in the total energy is zero: delta E equals delta K plus delta U equals 0. This gives the change in kinetic energy of the particle, delta K equals negative delta U equals 75 Joules. The change in the kinetic energy of the particle is delta e equals one half m v subscript f baseline squared minus one half m v subscript i baseline squared. Since the initial kinetic energy of the particle equals 0.0 Joules, one half m v squared equals seventy five j. Solving this equation using the given values and solving for the speed, v, results in v equals 5.0 meters per second.
. Solving this equation using the given values and solving for the speed, v, results in v = 5.0 m/s.
Correct Response: C. (Objective 0006) At x equals 1.0 m, the potential energy of the particle is 100 J. Since the particle is at rest, this is equal to its total energy. At x equals 4.0 m, the potential energy of the particle is 25 Joules, so the change in energy of the particle is delta E equals 25 Joules minus 100 Joules equals negative 75 Joules. Because there are no other forces acting, the total energy is conserved and the change in the total energy is zero: delta E equals delta K plus delta U equals 0. This gives the change in kinetic energy of the particle, delta K equals negative delta U equals 75 Joules. The change in the kinetic energy of the particle is delta e equals one half m v subscript f baseline squared minus one half m v subscript i baseline squared. Since the initial kinetic energy of the particle equals 0.0 Joules, one half m v squared equals seventy five j. Solving this equation using the given values and solving for the speed, v, results in v equals 5.0 meters per second.
Question 25
25. A spring with constant k is aligned in the vertical direction and has length L when uncompressed. A mass m is placed on the spring, compressing it distance x, as shown in the diagram below. The system is in equilibrium.
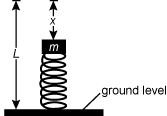
Which of the following equations represents the total energy of the mass with respect to the ground level?
- mgL + kx
- mgL +
 one half k x squared
one half k x squared
- mg(L − x) +
 one half k x squared
one half k x squared
- mgL +
 one half k times parens L minus x end parens squared
one half k times parens L minus x end parens squared
Answer to question 25
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0006) When the mass on the spring is compressed, the mass has gravitational potential energy with respect to the ground and elastic potential energy from the spring. Since the height of the mass above ground is L – x, the gravitational potential energy is mg (L – x). Since the spring is compressed distance x, the elastic potential energy of the mass on the spring is
 . The sum of these two is the total energy of the mass with respect to the ground level.
Correct Response: C. (Objective 0006) When the mass on the spring is compressed, the mass has gravitational potential energy with respect to the ground and elastic potential energy from the spring. Since the height of the mass above ground is L minus x, the gravitational potential energy is m g (L minus x). Since the spring is compressed distance x, the elastic potential energy of the mass on the spring is one half k x squared. The sum of these two is the total energy of the mass with respect to the ground level.
. The sum of these two is the total energy of the mass with respect to the ground level.
Correct Response: C. (Objective 0006) When the mass on the spring is compressed, the mass has gravitational potential energy with respect to the ground and elastic potential energy from the spring. Since the height of the mass above ground is L minus x, the gravitational potential energy is m g (L minus x). Since the spring is compressed distance x, the elastic potential energy of the mass on the spring is one half k x squared. The sum of these two is the total energy of the mass with respect to the ground level.
Question 26
26. A motor supplies 40 W to pull a 100
kg
mass up the entire length of a rough inclined plane having the dimensions shown in the diagram below.
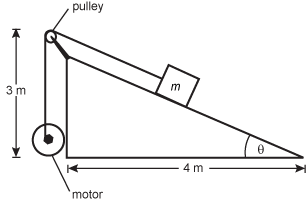
The incline has an angle of theta off the ground. On the left of the incline on the ground there is a motor that is connected to a pulley at the top of the incline. The distance from the base where the motor is up to the top of the pulley is three meters. There is a mass m half way up the incline labeled m and it is connected to the motor through the pulley with a rope.
The frictional force between the mass and the surface is a constant 200
N. How long will it take the motor to pull the mass up the incline?
- 25
s
- 73
s
- 88
s
- 99
s
Answer to question 26
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: D. (Objective 0006) Power is the rate of change of energy, or the rate at which work is done. Since the motor is supplying constant power, the rate is the total work divided by the time to do the work,
 . Solving for the time it will take to do the work gives
. Solving for the time it will take to do the work gives
 . The work required to pull the mass up the inclined plane is equal to the component of the net force in the direction of the displacement of the mass. The motor must do work against two forces acting on the mass: gravity and friction. The component of gravity down the inclined plane is mg sin θ, and the frictional force is a constant 200 N. Because the mass is moving up the incline, friction also acts down the incline. The distance over which the force acts is 5 m, since this distance is the hypotenuse of a 3-4-5 triangle. In addition,
. The work required to pull the mass up the inclined plane is equal to the component of the net force in the direction of the displacement of the mass. The motor must do work against two forces acting on the mass: gravity and friction. The component of gravity down the inclined plane is mg sin θ, and the frictional force is a constant 200 N. Because the mass is moving up the incline, friction also acts down the incline. The distance over which the force acts is 5 m, since this distance is the hypotenuse of a 3-4-5 triangle. In addition,
 . Therefore, the work done by the motor is given by force × distance = (5 m)(200 N + mg sin θ ) = (5 m)[200 N + (100 kg)(9.8 m/s2)(
. Therefore, the work done by the motor is given by force × distance = (5 m)(200 N + mg sin θ ) = (5 m)[200 N + (100 kg)(9.8 m/s2)( )] = 3940 J. The time required for the motor to do this work can be found by using the equation
)] = 3940 J. The time required for the motor to do this work can be found by using the equation
 .
Correct Response: D. (Objective 0006) Power is the rate of change of energy, or the rate at which work is done. Since the motor is supplying constant power, the rate is the total work divided by the time to do the work, p equals w over t.
.
Correct Response: D. (Objective 0006) Power is the rate of change of energy, or the rate at which work is done. Since the motor is supplying constant power, the rate is the total work divided by the time to do the work, p equals w over t.
Solving for the time it will take to do the work gives t equals w over p. The work required to pull the mass up the inclined plane is equal to the component of the net force in the direction of the displacement of the mass. The motor must do work against two forces acting on the mass: gravity and friction. The component of gravity down the inclined plane is mg sine theta, and the frictional force is a constant 200 Newtons. Because the mass is moving up the incline, friction also acts down the incline. The distance over which the force acts is 5 meters, since this distance is the hypotenuse of a 3-4-5 triangle. In addition, sine theta equals opposite over hypotenuse equals three over five.
Therefore, the work done by the motor is given by force times distance equals open parenthesis 5 meters close parenthesis open parenthesis 200 Newtons plus m g sine theta close parenthesis equals open parenthesis 5 meters close parenthesis left bracket 200 Newtons plus open parenthesis 100 kilograms close parenthesis open parenthesis 9.8 meters per second squared close parenthesis open parenthesis three fifths close parenthesis right bracket equals 3940 Joules. The time required for the motor to do this work can be found by using the equation t equals w over p equals three thousand nine hundred and forty j over forty w equals ninety nine s.
Question 27
27. The mechanical energy of moving wind, in the form of kinetic energy, is ultimately transformed into electrical energy by the generator in a wind turbine. Assume the wind incident on the blades of the turbine is modeled by a cylinder of air of mass m and cross-sectional area A. If v is the speed of the air, then the length of the cylinder is vΔ delta t, where Δ delta t is a small time interval. Which of the following gives the kinetic energy Ek of a volume of moving air in an interval Δ delta t, where ρ row = density of air and V is the volume of the cylinder?
- Ek =
 ρAv2E subscript k = one half row A v squared
ρAv2E subscript k = one half row A v squared
- Ek = ρAΔtv2E subscript k = row A delta t v squared
- Ek =
 ρAΔtv3E subscript k = row A delta t v cubed
ρAΔtv3E subscript k = row A delta t v cubed
- Ek =2ρAΔtv3E subscript k = 2 row A delta t v cubed
Answer to question 27
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0006) A moving mass of air has kinetic energy given by E =
 mv2. The mass of a given quantity of air m can be represented by using its density ρ and volume V by m = ρV. The volume of the air mass in a cylinder of length vΔt and cross-sectional area A is V = vΔtA. Substituting gives Ek =
mv2. The mass of a given quantity of air m can be represented by using its density ρ and volume V by m = ρV. The volume of the air mass in a cylinder of length vΔt and cross-sectional area A is V = vΔtA. Substituting gives Ek =
 mv2 =
mv2 =
 ρAΔtv3.
Correct Response: C. (Objective 0006) A moving mass of air has kinetic energy given by E = 1 half mv squared. The mass of a given quantity of air m can be represented by using its density row and volume V by m = row V. The volume of the air mass in a cylinder of length v delta t and cross-sectional area A is V = v delta t A. Substituting gives E subscript k = 1 half mv squared = 1 half row A delta tv cubed.
ρAΔtv3.
Correct Response: C. (Objective 0006) A moving mass of air has kinetic energy given by E = 1 half mv squared. The mass of a given quantity of air m can be represented by using its density row and volume V by m = row V. The volume of the air mass in a cylinder of length v delta t and cross-sectional area A is V = v delta t A. Substituting gives E subscript k = 1 half mv squared = 1 half row A delta tv cubed.
Question 28
28. A 2.0
kg
mass moving east at 5.0
m/s
strikes a 4.0
kg
mass at rest. The 2.0
kg
mass is deflected at a speed of 3.0
m/s
and an angle of 60° degrees north of east, as shown in the diagram below. Both masses are moving on frictionless ice.
before the collision mass one is on the left and has a mass of two point zero kilograms and a velocity of five point zero meters per second to the right horizontally. mass two has a mass of four point zero kilograms and has a velocity of zero point zero meters per second. after the collision mass one still has a mass of two point zero kilograms and is sixty degrees above the horizontal in a north east direction with a final velocity of three point zero meters per second. mass two still has a mass of four point zero kilograms and is some angle theta below the horizontal in a south east direction with an unknown velocity.
What is the final speed of the 4.0
kg
mass?
- 2.2
m/s
- 4.0
m/s
- 5.2
m/s
- 7.0
m/s
Answer to question 28
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: A. (Objective 0007) The interaction shown is a collision in two dimensions. The principle of conservation of momentum states that in the absence of external forces, the total momentum remains constant. Since momentum is a vector quantity, the momentum in the x-direction prior to the collision equals the momentum in the x-direction after the collision. The same is true in the y-direction. The magnitude of the momentum of a particle of mass m moving at speed v is p = mv. Prior to the collision, the total momentum of the system consisting of the two masses is in the x-direction only. Using an ordered pair to represent the vector momentum of a particle, the momentum before the collision is p1i + p2i = (2.0 kg × 5.0 m/s, 4.0 kg × 0.0 m/s) + (0.0 m/s, 0.0 m/s) = (10 kg-m/s, 0.0 kg-m/s). This must equal the final momentum of the two particles. According to the diagram after the collision, the final momentum of m1 is p2f = (6 cos 60°kg-m/s, 6 sin 60°kg-m/s) = (3 kg-m/s, 5.2 kg-m/s). Since p1i + p2i = p1f + p2f, then (10 mg-m/s, 0.0 kg-m/s) = (3 kg-m/s, 5.2 kg-m/s) + (p2xf, p2yf). Therefore (p2xf, p2yf) = (7 kg-m/s, –5.2 kg-m/s). The magnitude of this momentum vector is p2f = mv2f =
 . Dividing this by the mass of m2 = 4.0 kg gives the desired result of 2.2 m/s.
Correct Response: A. (Objective 0007) The interaction shown is a collision in two dimensions. The principle of conservation of momentum states that in the absence of external forces, the total momentum remains constant.
. Dividing this by the mass of m2 = 4.0 kg gives the desired result of 2.2 m/s.
Correct Response: A. (Objective 0007) The interaction shown is a collision in two dimensions. The principle of conservation of momentum states that in the absence of external forces, the total momentum remains constant.
Since momentum is a vector quantity, the momentum in the x-direction prior to the collision equals the momentum in the x-direction after the collision. The same is true in the y-direction. The magnitude of the momentum of a particle of mass m moving at speed v is p equals m v.
Prior to the collision, the total momentum of the system consisting of the two masses is in the x-direction only. Using an ordered pair to represent the vector momentum of a particle, the momentum before the collision is p subscript one i baseline plus p subscript two i equals open parenthesis 2.0 k g times 5.0 m slash s, 4.0 k g times 0.0 meters per second close parenthesis plus open parenthesis 0.0 meters per second, 0.0 meters per second close parenthesis equals open parenthesis 10 kilogram-meters per second, 0.0 kilogram-meters per second close parenthesis. This must equal the final momentum of the two particles.
According to the diagram after the collision, the final momentum of m subscript one is p subscript two f equals open parenthesis 6 cosine 60 degrees kilogram meters per second, 6 sine 60 degrees kilogram meters per second close parenthesis equals open parenthesis 3 kilogram meters per second, 5.2 kilogram meters per second close parenthesis. Since p subscript one i plus p subscript two i equals psubscript one f plus p subscript two f, then open parenthesis 10 mg-meters per second, 0.0 kilogram meters per second close parenthesis equals open parenthesis 3 kilogram meters per second, 5.2 kilogram meters per second close parenthesis plus open parenthesis p subscript two x f baseline comma p subscript two y f baseline close parenthesis.
Therefore open parenthesis p subscript two x f baseline comma p subscript two y f baseline close parenthesis equals open parenthesis 7 kilogram meters per second, negative 5.2 kilogram meters per second close parenthesis. The magnitude of this momentum vector is p subscript two f equals mv subscript two f baseline equals start square root open parenthesis seven kilogram meters per second close parenthesis squared plus open parenthesis negative five point two kilogram meters per second close parenthesis squared end root equals eight point eight kilogram meters per second. Dividing this by the mass of m subscript two equals 4.0 kilogram gives the desired result of 2.2 meters per second.
Question 29
29. A spherical star of radius R0 subscript 0 rotates about its axis at an angular speed of ω0 omega subscript 0 . The star expands to a spherical star of radius 2R0 with the same mass distribution. What is the final angular speed of rotation?
-
 one forth omega subscript 0
one forth omega subscript 0
-
 one half omega subscript 0
one half omega subscript 0
-
 square root of 2 over 2 omega subscript 0
square root of 2 over 2 omega subscript 0
- ω0 omega subscript 0
Answer to question 29
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: A. (Objective 0007) The principle of conservation of angular momentum states that in the absence of external torques, the total angular momentum of a system remains constant. One expression for the angular momentum, L, of an object is L = Iω, where I is the moment of inertia and ω is its angular speed. The moment of inertia of an object depends on how the mass is distributed with respect to its rotational axis. For a discrete mass distribution, it is given by I = ∑ miri2
. For the continuous case, it is given by an integral. In either case, the moment of inertia depends on the square of the distance of each mass particle from its rotational axis. In the case of a sphere, if the radius of the sphere doubles while the total mass and mass distribution remain the same, the moment of inertia will increase by a factor of 4, since 22 = 4. Therefore, if I0 equals the initial moment of inertia of the star, the moment of inertia of the expanded star will be 4I0. The equation for conservation of angular momentum for this system then becomes I0ω0 = 4I0ωf , where ωf equals the final angular speed. Solving this equation for ωf gives the answer of
 .
Correct Response: A. (Objective 0007) The principle of conservation of angular momentum states that in the absence of external torques, the total angular momentum of a system remains constant. One expression for the angular momentum, L, of an object is L equals I omega, where I is the moment of inertia and omega is its angular speed. The moment of inertia of an object depends on how the mass is distributed with respect to its rotational axis. For a discrete mass distribution, it is given by I equals sigma m subscript i r subscript i squared. For the continuous case, it is given by an integral. In either case, the moment of inertia depends on the square of the distance of each mass particle from its rotational axis. In the case of a sphere, if the radius of the sphere doubles while the total mass and mass distribution remain the same, the moment of inertia will increase by a factor of 4, since 22 equals 4. Therefore, if I subscript zero equals the initial moment of inertia of the star, the moment of inertia of the expanded star will be 4 I subscript zero. The equation for conservation of angular momentum for this system then becomes I subscript zero omega subscript zero equals 4 I subscript zero omega subscript f, where omega subscript f equals the final angular speed. Solving this equation for omega subscript f gives the answer of one fourth omega subscript zero.
.
Correct Response: A. (Objective 0007) The principle of conservation of angular momentum states that in the absence of external torques, the total angular momentum of a system remains constant. One expression for the angular momentum, L, of an object is L equals I omega, where I is the moment of inertia and omega is its angular speed. The moment of inertia of an object depends on how the mass is distributed with respect to its rotational axis. For a discrete mass distribution, it is given by I equals sigma m subscript i r subscript i squared. For the continuous case, it is given by an integral. In either case, the moment of inertia depends on the square of the distance of each mass particle from its rotational axis. In the case of a sphere, if the radius of the sphere doubles while the total mass and mass distribution remain the same, the moment of inertia will increase by a factor of 4, since 22 equals 4. Therefore, if I subscript zero equals the initial moment of inertia of the star, the moment of inertia of the expanded star will be 4 I subscript zero. The equation for conservation of angular momentum for this system then becomes I subscript zero omega subscript zero equals 4 I subscript zero omega subscript f, where omega subscript f equals the final angular speed. Solving this equation for omega subscript f gives the answer of one fourth omega subscript zero.
Question 30
30. A 2.0
kg
mass moving at 6.0 meters per second collides with a 1.0
kg
mass at rest. The masses are traveling on a frictionless surface and the collision occurs in one dimension. After the collision, the two masses become joined and move off together. How much energy is dissipated in this collision?
- 0.0
J
- 8.0
J
- 12
J
- 36
J
Answer to question 30
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0007) Solving this problem requires comparing the kinetic energy prior to the collision with the kinetic energy after the collision. To find the final kinetic energy it is necessary to find the final speed of the two masses. Because the surface on which the masses are moving is frictionless, the only kinetic energy lost will be due to the work done by internal forces acting during the collision. Since momentum is conserved, the momentum before the collision must equal the momentum after the collision. Because the masses are stuck together, the masses have the same final speed. Let v represent the final speed. Then (2.0 kg)(6.0 m/s) + (1.0 kg)(0.0 m/s) = (2.0 kg)v + (1.0 kg)v = (3.0 kg)v, and v = 4.0 m/s. The kinetic energy before the collision is KEi =
 . The kinetic energy after the collision is KEf =
. The kinetic energy after the collision is KEf =
 . Therefore, the change in energy is KEf – KEi = 36 J – 24 J = 12 J.
Correct Response: C. (Objective 0007) Solving this problem requires comparing the kinetic energy prior to the collision with the kinetic energy after the collision. To find the final kinetic energy it is necessary to find the final speed of the two masses. Because the surface on which the masses are moving is frictionless, the only kinetic energy lost will be due to the work done by internal forces acting during the collision. Since momentum is conserved, the momentum before the collision must equal the momentum after the collision. Because the masses are stuck together, the masses have the same final speed. Let v represent the final speed. Then open parenthesis 2.0 kilograms close parenthesis open parenthesis 6.0 meters per second close parenthesis plus open parenthesis 1.0 kilograms close parenthesis open parenthesis 0.0 meters per second close parenthesis equals open parenthesis 2.0 kilograms close parenthesis v plus open parenthesis 1.0 kilograms close parenthesis v equals open parenthesis 3.0 kilograms close parenthesis v, and v equals 4.0 meters per second. The kinetic energy before the collision is K E subscript i equals one half m v squared equals one half open parenthesis two point zero kilograms close parenthesis open parenthesis six point zero m slash s close parenthesis squared equals thirty six j. The kinetic energy after the collision is K E subscript f equals one half m v squared equals one half open parenthesis three point zero kilograms close parenthesis open parenthesis four point zero m slash s close parenthesis squared equals twenty four j. Therefore, the change in energy is K E subscript f baseline minus K E subscript i equals 36 Joules minus 24 Joules equals 12 Joules.
. Therefore, the change in energy is KEf – KEi = 36 J – 24 J = 12 J.
Correct Response: C. (Objective 0007) Solving this problem requires comparing the kinetic energy prior to the collision with the kinetic energy after the collision. To find the final kinetic energy it is necessary to find the final speed of the two masses. Because the surface on which the masses are moving is frictionless, the only kinetic energy lost will be due to the work done by internal forces acting during the collision. Since momentum is conserved, the momentum before the collision must equal the momentum after the collision. Because the masses are stuck together, the masses have the same final speed. Let v represent the final speed. Then open parenthesis 2.0 kilograms close parenthesis open parenthesis 6.0 meters per second close parenthesis plus open parenthesis 1.0 kilograms close parenthesis open parenthesis 0.0 meters per second close parenthesis equals open parenthesis 2.0 kilograms close parenthesis v plus open parenthesis 1.0 kilograms close parenthesis v equals open parenthesis 3.0 kilograms close parenthesis v, and v equals 4.0 meters per second. The kinetic energy before the collision is K E subscript i equals one half m v squared equals one half open parenthesis two point zero kilograms close parenthesis open parenthesis six point zero m slash s close parenthesis squared equals thirty six j. The kinetic energy after the collision is K E subscript f equals one half m v squared equals one half open parenthesis three point zero kilograms close parenthesis open parenthesis four point zero m slash s close parenthesis squared equals twenty four j. Therefore, the change in energy is K E subscript f baseline minus K E subscript i equals 36 Joules minus 24 Joules equals 12 Joules.
Question 31
31. John (m = 80
kg) and Mary (m = 55
kg) are riding in bumper cars at an amusement park. Both cars have the same mass, 150
kg. While John's car is at rest, Mary's approaches at a speed of 2.1
m/s
and strikes the back of his car. John's car moves forward with a speed of 1.2
m/s. Assuming Mary lifts her foot from the speed control at the time of impact, and her car continues to move forward in line with John's car, what is the final speed of her car after the collision?
- 0.76
m/s
- 1.2
m/s
- 1.4
m/s
- 2.1
m/s
Answer to question 31
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: A. (Objective 0007) Momentum is conserved, so the initial momentum equals the final momentum, Pi = Pf. The initial momentum (before the collision) is Pi = (m1 • v1i) + (m2 • v2i) and the final momentum Pf = (m1 • v1f) + (m2 • v2f) (after collision). Using the values, Pi = (55 kg + 150 kg) (2.10 m/s) + (80 kg + 150 kg) (0 m/s) = 431 kg•m/s and Pf = (80 kg + 150 kg) × (1.2 m/s) + (55 kg + 150 kg)v2f = 431 kg•m/s. Solving for v2f, the final speed of Mary and her car gives v2f = 0.76 m/s.
Correct Response: A. (Objective 0007) Momentum is conserved, so the initial momentum equals the final momentum, P subscript i = P subscript f. The initial momentum (before the collision) is P subscript i = (m subscript 1 times v subscript 1i) + (m subscript 2 times v subscript 2i) and the final momentum P subscript f = (m subscript 1 times v subscript 1f) + (m2 times v subscript 2f) (after collision). Using the values, P subscript i = (55 kilogram + 150 kilogram ) (2.10 meters per second ) + (80 kilogram + 150 kilogram ) (0 meters per second ) = 431 kilogram meters per second and P subscript f = (80 kilogram + 150 kilogram ) times (1.2 meters per second) + (55 kilogram + 150 kilogram )v subscript 2f = 431 kilogram meters per second. Solving for v subscript 2f, the final speed of Mary and her car gives v subscript 2f = 0.76 meters per second.
Question 32
32. The graph below shows the motion of a 2 kg mass undergoing simple harmonic motion.

What is the magnitude of the maximum value of the restoring force on the mass?
32. The graph shows the motion of a two kilogram mass undergoing simple harmonic motion.
An x-y coordinate system is shown. The y-axis (vertical) is labeled Displacement with meters in parentheses. The tick marks go from negative six meters to positive six meters . The x-axis is labeled Time with seconds in parentheses. The tick marks go from zero seconds to fifteen seconds.
At time equals zero seconds the curve is at a displacement of four meters. The curve moves downwards and to the right to cross the time-axis at time equals two seconds and displacement equals zero meters. The curve continues downwards and to the right to a local minimum at time equals four seconds and displacement equals negative four meters. The curve then starts upwards and to the right to cross the time axis at time equals six seconds and displacement equals zero meters. The curve continues upwards and to the right to reach a local maximum at time equals eight seconds and displacement equals four meters. The curve then moves downwards and to the right to cross the time-axis at time equals ten seconds and displacement equals zero meters. The curve continues downwards and to the right to reach a local minimum at time equals twelve seconds and displacement equals negative four meters. The curve then moves upwards and to the right to intersect the time axis at time equals fourteen seconds and displacement equals zero meters. The curve terminates at this point.
What is the magnitude of the maximum value of the restoring force on the mass?
-
 N
N
-
 N
N
-
 N
N
-
 N
N
Answer to question 32
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: A. (Objective 0008) We can write the equation of the graph as
 where A is the amplitude and T is the period. Differentiating this twice gives a formula for the acceleration of the mass
where A is the amplitude and T is the period. Differentiating this twice gives a formula for the acceleration of the mass
 . So the maximum acceleration of the mass is
. So the maximum acceleration of the mass is
 and using Newton's second, law the maximum value of the restoring force is
and using Newton's second, law the maximum value of the restoring force is
 . Substituting the data into the equation gives the desired result.
Correct Response: A. (Objective 0008) We can write the equation of the graph as x of t equals A cosine 2pi t over upper T where A is the amplitude and T is the period. Differentiating this twice gives a formula for the acceleration of the mass a of t = negative upper A (2 pi over upper T) squared cosine (2 pi t over upper T). So the maximum acceleration of the mass is a subscript max = upper A(2 pi over upper T) squared and using Newton's second, law the maximum value of the restoring force is upper F subscript max = ma subscript max = m upper A(2 pi over upper T) squared. Substituting the data into the equation gives the desired result.
. Substituting the data into the equation gives the desired result.
Correct Response: A. (Objective 0008) We can write the equation of the graph as x of t equals A cosine 2pi t over upper T where A is the amplitude and T is the period. Differentiating this twice gives a formula for the acceleration of the mass a of t = negative upper A (2 pi over upper T) squared cosine (2 pi t over upper T). So the maximum acceleration of the mass is a subscript max = upper A(2 pi over upper T) squared and using Newton's second, law the maximum value of the restoring force is upper F subscript max = ma subscript max = m upper A(2 pi over upper T) squared. Substituting the data into the equation gives the desired result.
Question 33
33. A mass attached to a spring oscillates on a horizontal, frictionless surface. The graph below shows how the magnitude of the force of the spring on the mass depends on the distance, x, the spring is displaced.
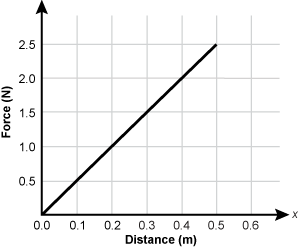
starting at the origin increasing steadily passing through open parenthesis zero point one comma zero point five close parenthesis then passing open parenthesis zero point two comma one point zero close parenthesis and continuing the same increase up to open parenthesis zero point five comma two point five close parenthesis where the data ends
Given that m = 0.20
kg
and the mass is extended 0.4
m
and released from rest at t = 0.0
s, which of the following equations describes the position, x, in meters, of the mass with respect to time, t, in seconds?
- x = 0.2
cos
0.4t
- x = 0.2
cos
0.8t
- x = 0.4
cos
2t
- x = 0.4
cos
5t
Answer to question 33
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: D. (Objective 0008) When a mass is attached to a spring and displaced, the system will undergo simple harmonic motion. In this case, the mass oscillates back and forth in the horizontal direction with no energy loss due to friction. Since the spring is extended at t = 0.0 s, the displacement is represented by the cosine function and can be written as x = A cos (ω t + φ ), where x is the displacement of the particle, A is the amplitude of motion, ω is the angular frequency, and φ is the phase constant. For a mass on a spring the amplitude represents the maximum displacement of the mass on the spring, which is given, so A = 0.4 m. The angular speed is
 , where k is the spring constant and m is the mass on the spring. According to Hooke's law, the magnitude of the force on the mass is related to the magnitude of the displacement and given by F = kx, so the value of k is equal to the slope of the line, or k = 5.0 N/m. Substituting these two values gives
ω = 5rad/s. Finally, the phase constant equals 0, since the object is released from rest at t = 0.0 s. Substituting the values found into the above displacement equation results in x = 0.4 cos 5t.
Correct Response: D. (Objective 0008) When a mass is attached to a spring and displaced, the system will undergo simple harmonic motion.
, where k is the spring constant and m is the mass on the spring. According to Hooke's law, the magnitude of the force on the mass is related to the magnitude of the displacement and given by F = kx, so the value of k is equal to the slope of the line, or k = 5.0 N/m. Substituting these two values gives
ω = 5rad/s. Finally, the phase constant equals 0, since the object is released from rest at t = 0.0 s. Substituting the values found into the above displacement equation results in x = 0.4 cos 5t.
Correct Response: D. (Objective 0008) When a mass is attached to a spring and displaced, the system will undergo simple harmonic motion.
In this case, the mass oscillates back and forth in the horizontal direction with no energy loss due to friction. Since the spring is extended at t equals 0.0 seconds, the displacement is represented by the cosine function and can be written as x equals A cosine open parenthesis omega t plus phi close parenthesis, where x is the displacement of the particle, A is the amplitude of motion, omega is the angular frequency, and phi is the phase constant. For a mass on a spring the amplitude represents the maximum displacement of the mass on the spring, which is given, so A equals 0.4 meters. The angular speed is omega equals square root of k over m, where k is the spring constant and m is the mass on the spring. According to Hooke's law, the magnitude of the force on the mass is related to the magnitude of the displacement and given by F equals k x, so the value of k is equal to the slope of the line, or k equals 5.0 Newtons per meter.
Substituting these two values gives omega equals 5 radians per second. Finally, the phase constant equals 0, since the object is released from rest at t equals 0.0 seconds. Substituting the values found into the above displacement equation results in x equals 0.4 cosine 5 t.
Question 34
34. The diagram below shows the position of a mass on a spring with respect to time undergoing simple harmonic motion.
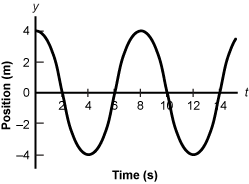
wavy graph. starting at open parenthesis zero comma four close parenthesis and decreasing down to open parenthesis two comma zero close parenthesis passing into the fourth quadrant down to open parenthesis four comma negative four close parenthesis where it peaks in a curved fashion and starts increasing back up to the x axis at open parenthesis six comma zero close parenthesis increasing into the first quadrant up to open parenthesis eight comma four close parenthesis where it peaks in a curved fashion and then decreases back to the x axis at open parenthesis ten comma zero close parenthesis where it decrease back into the fourth quadrant and peaks in a curved fashion down to open parenthesis twelve comma negative four close parenthesis then starts increasing back up to the x axis at open parenthesis fourteen comma zero close parenthesis and continues to increase into the first quadrant.
If the spring constant is given by k = 6
N/m, what is the maximum kinetic energy of the mass on the spring?
- 12
J
- 16
J
- 24
J
- 48
J
Answer to question 34
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: D. (Objective 0008) For a mass undergoing simple harmonic motion, the total energy is constant and is given by
 . When the mass is at its maximum displacement from the equilibrium position, its speed is zero and all of the energy is potential energy. According to the graph, the maximum displacement is x = 4 m. Therefore, when x = 4 m the speed is v = 0 m/s and the total energy is
. When the mass is at its maximum displacement from the equilibrium position, its speed is zero and all of the energy is potential energy. According to the graph, the maximum displacement is x = 4 m. Therefore, when x = 4 m the speed is v = 0 m/s and the total energy is
 . When the mass passes through the origin, its kinetic energy is maximum and its potential energy is zero, since x = 0 m. Since the total energy is constant, the maximum kinetic energy is equal to the maximum potential energy, which is 48 J.
Correct Response: D. (Objective 0008) For a mass undergoing simple harmonic motion, the total energy is constant and is given by e equals one half m v squared plus one half k x squared. When the mass is at its maximum displacement from the equilibrium position, its speed is zero and all of the energy is potential energy. According to the graph, the maximum displacement is x equals 4 meters. Therefore, when x equals 4 meters the speed is v equals 0 meters per second and the total energy is e equals one half m open parenthesis zero m slash s close parenthesis squared plus one half k x squared equals one half open parenthesis six n slash m close parenthesis open parenthesis four m close parenthesis squared equals forty eight j. When the mass passes through the origin, its kinetic energy is maximum and its potential energy is zero, since x equals 0 meters. Since the total energy is constant, the maximum kinetic energy is equal to the maximum potential energy, which is 48 Joules.
. When the mass passes through the origin, its kinetic energy is maximum and its potential energy is zero, since x = 0 m. Since the total energy is constant, the maximum kinetic energy is equal to the maximum potential energy, which is 48 J.
Correct Response: D. (Objective 0008) For a mass undergoing simple harmonic motion, the total energy is constant and is given by e equals one half m v squared plus one half k x squared. When the mass is at its maximum displacement from the equilibrium position, its speed is zero and all of the energy is potential energy. According to the graph, the maximum displacement is x equals 4 meters. Therefore, when x equals 4 meters the speed is v equals 0 meters per second and the total energy is e equals one half m open parenthesis zero m slash s close parenthesis squared plus one half k x squared equals one half open parenthesis six n slash m close parenthesis open parenthesis four m close parenthesis squared equals forty eight j. When the mass passes through the origin, its kinetic energy is maximum and its potential energy is zero, since x equals 0 meters. Since the total energy is constant, the maximum kinetic energy is equal to the maximum potential energy, which is 48 Joules.
Question 35
35. A child is on a swing with ropes that are 3
m
long. The child's parent stands behind the swing and pushes the child on it. Approximately how often will the parent need to push to maximize the amplitude of the child's motion?
- once every 0.29
s
- once every 1.7
s
- once every 3.0
s
- once every 3.5
s
Answer to question 35
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: D. (Objective 0008) A pendulum undergoes simple harmonic motion for small displacements, since the restoring force is approximately linear and in the opposite direction of the displacement. A driven oscillating system will achieve resonance, or maximum amplitude, when the frequency of the driving force is equal to the resonant frequency of the system. In the case of the pendulum, the resonant frequency is the reciprocal of its period, and the period is
 Since the frequency is the reciprocal of the period, the parent will need to push the swing once every 3.5 s to maximize the amplitude of the child's motion.
Correct Response: D. (Objective 0008) A pendulum undergoes simple harmonic motion for small displacements, since the restoring force is approximately linear and in the opposite direction of the displacement. A driven oscillating system will achieve resonance, or maximum amplitude, when the frequency of the driving force is equal to the resonant frequency of the system. In the case of the pendulum, the resonant frequency is the reciprocal of its period, and the period is upper t equals two pi square root l over g equals two pi square root of three m over nine point eight m slash s squared is approximately equals to three point five s. Since the frequency is the reciprocal of the period, the parent will need to push the swing once every 3.5 seconds to maximize the amplitude of the child's motion.
Since the frequency is the reciprocal of the period, the parent will need to push the swing once every 3.5 s to maximize the amplitude of the child's motion.
Correct Response: D. (Objective 0008) A pendulum undergoes simple harmonic motion for small displacements, since the restoring force is approximately linear and in the opposite direction of the displacement. A driven oscillating system will achieve resonance, or maximum amplitude, when the frequency of the driving force is equal to the resonant frequency of the system. In the case of the pendulum, the resonant frequency is the reciprocal of its period, and the period is upper t equals two pi square root l over g equals two pi square root of three m over nine point eight m slash s squared is approximately equals to three point five s. Since the frequency is the reciprocal of the period, the parent will need to push the swing once every 3.5 seconds to maximize the amplitude of the child's motion.
Question 36
36. A system consists of a mass m is attached to a spring with constant k. The mass is free to move on a frictionless horizontal surface. After being compressed to a length xOsubscript O, the mass oscillates about a central point at a frequency of 100
Hz. The system is stopped and the mass is replaced with a mass of 2m, compressed the same distance and released. What is the new frequency of the system?
- 35
Hz
- 50
Hz
- 71
Hz
- 100
Hz
Answer to question 36
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0008) The force on the mass is F = ma = –kx. Since the acceleration is proportional to the displacement and in the opposite direction, the system will undergo periodic motion and oscillate with angular frequency
 . This frequency is given in radians per second. Converting to Hz (cycles per second) gives
. This frequency is given in radians per second. Converting to Hz (cycles per second) gives
 . From inspection, doubling the mass will result in the frequency changing by a factor of
. From inspection, doubling the mass will result in the frequency changing by a factor of
 .
Correct Response: C. (Objective 0008) The force on the mass is F = m a = negative kx. Since the acceleration is proportional to the displacement and in the opposite direction, the system will undergo periodic motion and oscillate with angular frequency omega equals the square root of k over m. This frequency is given in radians per second. Converting to hertz (cycles per second) gives frequency equals 1 over 2 pi times the square root of k over m. From inspection, doubling the mass will result in the frequency changing by a factor of 1 over the square root of 2.
.
Correct Response: C. (Objective 0008) The force on the mass is F = m a = negative kx. Since the acceleration is proportional to the displacement and in the opposite direction, the system will undergo periodic motion and oscillate with angular frequency omega equals the square root of k over m. This frequency is given in radians per second. Converting to hertz (cycles per second) gives frequency equals 1 over 2 pi times the square root of k over m. From inspection, doubling the mass will result in the frequency changing by a factor of 1 over the square root of 2.
Question 37
37. The diagram below shows a standing wave on a string with both ends fixed.
The diagram shows a sine wave on a string fixed at both ends and with a peak then a trough then another peak, all of equal length and displacement. The total length is shown as one point zero m.
If the length of the string is 1.0
m
and the wave speed in the string is 200
m/s, what is the frequency of the wave?
- 100
Hz
- 150
Hz
- 200
Hz
- 300
Hz
Answer to question 37
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: D. (Objective 0009) A standing wave is generated in a string fixed at both ends and the given wave speed is 200 m/s. According to the diagram, the wave is oscillating in one of its harmonics and the wavelength is two-thirds of the length of the string, or
 m. For any wave, v = fλ, where v is the wave speed, f is the frequency, and λ is the wavelength. Therefore,
m. For any wave, v = fλ, where v is the wave speed, f is the frequency, and λ is the wavelength. Therefore,
 Correct Response: D. (Objective 0009) A standing wave is generated in a string fixed at both ends and the given wave speed is 200 meters per second. According to the diagram, the wave is oscillating in one of its harmonics and the wavelength is two-thirds of the length of the string, or two thirds meters. For any wave, v equals f lambda, where v is the wave speed, f is the frequency, and lambda is the wavelength. Therefore, f equals v over lambda equals two hundred m slash s divided by two thirds m equals three hundred H z.
Correct Response: D. (Objective 0009) A standing wave is generated in a string fixed at both ends and the given wave speed is 200 meters per second. According to the diagram, the wave is oscillating in one of its harmonics and the wavelength is two-thirds of the length of the string, or two thirds meters. For any wave, v equals f lambda, where v is the wave speed, f is the frequency, and lambda is the wavelength. Therefore, f equals v over lambda equals two hundred m slash s divided by two thirds m equals three hundred H z.
Question 38
38. The diagram below shows a snapshot at t = 0
s
of two wave pulses, each moving in the direction indicated at a speed of 1 unit per second.
The first is a waveform at position x equals three with a peak of height one unit. An arrow indicated movement to the right. The second waveform has a peak of one square unit magnitude at x equals seven and then a valley of one square magnitude at x equals eight. An arrow indicates this waveform is moving to the left.
Which of the following diagrams shows the wave pulses at t = 2
s?
-
-
-
-
Answer to question 38
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: B. (Objective 0009) The diagram shows two wave pulses traveling in opposite directions. According to the superposition principle, when two waves interfere, the displacement of the resulting wave at any point is the algebraic sum of the individual waves. Since the waves are each traveling at 1 unit per second, each wave pulse will travel two units in two seconds. Drawing the new position of the wave pulses and finding their sum results in a wave pulse that has one part displaced two units above the x-axis and the other part displaced one unit below the x-axis.
Correct Response: B. (Objective 0009) The diagram shows two wave pulses traveling in opposite directions. According to the superposition principle, when two waves interfere, the displacement of the resulting wave at any point is the algebraic sum of the individual waves. Since the waves are each traveling at 1 unit per second, each wave pulse will travel two units in two seconds. Drawing the new position of the wave pulses and finding their sum results in a wave pulse that has one part displaced two units above the x axis and the other part displaced one unit below the x axis.
Question 39
39. The diagram below shows a wave pulse on a thin string that is attached to a thick string. The linear density of the thin string is less than the linear density of the thick string. The tension in the two strings is the same.
A single wave peak is shown traveling in the thin string with an arrow showing movement toward the thick string.
Which of the following diagrams best represents this situation after the wave pulse interacts with the boundary of the two wave mediums?
-
 The diagram of the thin and thick strings shows a wave trough traveling in the thin string with an arrow showing movement away from the thick string, and a single wave peak is traveling in the thick string with an arrow indicating motion away from the thin string.
The diagram of the thin and thick strings shows a wave trough traveling in the thin string with an arrow showing movement away from the thick string, and a single wave peak is traveling in the thick string with an arrow indicating motion away from the thin string.
-
 The diagram of the thin and thick strings shows a wave trough traveling in the thin string with an arrow showing movement away from the thick string, and a single wave trough is traveling in the thick string with an arrow indicating motion away from the thin string.
The diagram of the thin and thick strings shows a wave trough traveling in the thin string with an arrow showing movement away from the thick string, and a single wave trough is traveling in the thick string with an arrow indicating motion away from the thin string.
-
 The diagram of the thin and thick strings shows a wave peak traveling in the thin string with an arrow showing movement away from the thick string, and a single wave peak is traveling in the thick string with an arrow indicating motion away from the thin string.
The diagram of the thin and thick strings shows a wave peak traveling in the thin string with an arrow showing movement away from the thick string, and a single wave peak is traveling in the thick string with an arrow indicating motion away from the thin string.
-
 The diagram of the thin and thick strings shows a wave peak traveling in the thin string with an arrow showing movement away from the thick string, and a single wave trough is traveling in the thick string with an arrow indicating motion away from the thin string.
The diagram of the thin and thick strings shows a wave peak traveling in the thin string with an arrow showing movement away from the thick string, and a single wave trough is traveling in the thick string with an arrow indicating motion away from the thin string.
Answer to question 39
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: A. (Objective 0009) When the wave pulse traveling in the less dense medium (the thin string) interacts with the boundary of a medium having a greater density (the thick string), part of the wave will be reflected and part of the wave will be transmitted to the denser medium. When the wave pulse on the thin string interacts with the thicker string, there will be a net force in the upward direction on the thicker string. The transmitted pulse will therefore be upright and travel to the right. According to Newton's third law, there will be an equal and opposite force on the particles in the less dense string. Because the particles in the less dense string have less mass, this force will accelerate the particles downward in the less dense string, resulting in an inverted pulse.
Correct Response: A. (Objective 0009) When the wave pulse traveling in the less dense medium (the thin string) interacts with the boundary of a medium having a greater density (the thick string), part of the wave will be reflected and part of the wave will be transmitted to the denser medium. When the wave pulse on the thin string interacts with the thicker string, there will be a net force in the upward direction on the thicker string. The transmitted pulse will therefore be upright and travel to the right. According to Newton's third law, there will be an equal and opposite force on the particles in the less dense string. Because the particles in the less dense string have less mass, this force will accelerate the particles downward in the less dense string, resulting in an inverted pulse.
Question 40
40. A person is sending a travelling wave down a long horizontal string by shaking one end of the string up and down in the vertical direction. Which of the following statements about the wave pulse on the string is true?
- Increasing the tension in the string will increase the frequency of the wave.
- Increasing the linear density of the string will increase the speed of the wave.
- Increasing the size of the vertical displacement will increase the energy of the wave.
- Increasing the rate at which the string moves up and down will increase the amplitude of the wave.
Answer to question 40
-
AnswerAnswer. Click to expand or collapse.
- Correct Response: C. (Objective 0009) Increasing the size of the up and down displacement in the vertical direction will increase the amplitude of the wave. Since the energy of a wave is proportional the square of the amplitude, increasing the amplitude will increase the energy of the wave.
Correct Response: C. (Objective 0009) Increasing the size of the up and down displacement in the vertical direction will increase the amplitude of the wave. Since the energy of a wave is proportional the square of the amplitude, increasing the amplitude will increase the energy of the wave.