Mathematics (Grades 5–12)
Subtest 2 Sample Items
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Expand All | Collapse All
Question 1
1. A 26 ft. clothesline reaches across a city alley from a 5th floor window in
one building to a 4th floor window in another building. If the vertical drop between the windows is
10 ft., what is the approximate angle of elevation, θ, of the clothesline?1.
A 26 foot clothesline reaches across a city alley from a fifth floor window in one building
to a fourth floor window in another building. If the vertical drop between the windows is 10 feet,
what is the approximate angle of elevation, theta, of the clothesline?
- 21°21 degrees
- 23°23 degrees
- 67°67 degrees
- 69°69 degrees
Answer to question 1
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0008) The situation can be represented
by a right triangle with one leg parallel to the ground, the other leg equal to the vertical drop from
the 5th floor window to the 4th floor window, and the hypotenuse equal to the length of the clothesline.
The angle of elevation is the angle between the leg parallel to the ground and the hypotenuse. Using
the sine ratio,
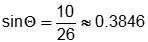 and using inverse sine, sin–1(0.3846) ≈ 23°.
Correct Response: B. (Objective 0008) The situation can be represented
by a right triangle with one leg parallel to the ground, the other leg equal to the vertical drop from
the 5th floor window to the 4th floor window, and the hypotenuse equal to the length of the clothesline.
The angle of elevation is the angle between the leg parallel to the ground and the hypotenuse. Using
the sine ratio, sin of theta equals ten twenty sixths which approximately equals zero point three eight
four six and using inverse sine, sine superscript negative 1 ( 0 point 3846 ) almost equal to 23 degrees.
and using inverse sine, sin–1(0.3846) ≈ 23°.
Correct Response: B. (Objective 0008) The situation can be represented
by a right triangle with one leg parallel to the ground, the other leg equal to the vertical drop from
the 5th floor window to the 4th floor window, and the hypotenuse equal to the length of the clothesline.
The angle of elevation is the angle between the leg parallel to the ground and the hypotenuse. Using
the sine ratio, sin of theta equals ten twenty sixths which approximately equals zero point three eight
four six and using inverse sine, sine superscript negative 1 ( 0 point 3846 ) almost equal to 23 degrees.
Question 2
2. A human body that weighs 160 pounds contains 5 liters of blood. If the density of blood is 1060 kg/m3kiligrams per meter cubed, one liter is 0.001 m30 point 001
meter cubed, and one kilogram weighs approximately 2.2 pounds, approximately what percentage
of the body weight is blood?
- 1.5 %1 point 5 percent
- 7.3 %7 point 3 percent
- 45 %45 percent
- 72 %72 percent
Answer to question 2
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0008)
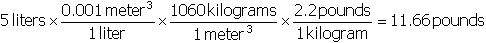
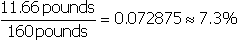 Correct Response: B. (Objective 0008) five liters times start fraction numerator
zero point zero zero one meters cubed denominator one liter end fraction times start fraction one thousand
sixty kilograms denominator one meters cubed end fraction times start fraction numerator two point two
pounds denominator one kilogram end fraction equals eleven point six six pounds start fraction numerator
eleven point six six pounds denominator one hundred and sixty pounds end fraction equals zero point
zero seven two eight seven five or approximately seven point three percent
Correct Response: B. (Objective 0008) five liters times start fraction numerator
zero point zero zero one meters cubed denominator one liter end fraction times start fraction one thousand
sixty kilograms denominator one meters cubed end fraction times start fraction numerator two point two
pounds denominator one kilogram end fraction equals eleven point six six pounds start fraction numerator
eleven point six six pounds denominator one hundred and sixty pounds end fraction equals zero point
zero seven two eight seven five or approximately seven point three percent
Question 3
3. A ladder leaning against a wall makes a 20° degree angle with the ground. When the bottom of the ladder
is moved 2
ft.
closer to the wall, the ladder makes a 40° degree angle with the ground. Approximately how long is the
ladder?
- 8.5
ft.
- 10
ft.
- 11.5
ft.
- 13
ft.
Answer to question 3
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0008) This problem can be represented
by a diagram, as shown below.
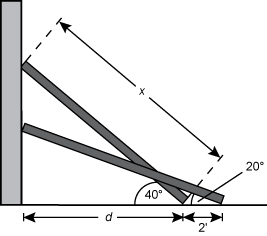
In the diagram, x represents the length of the ladder, and d represents the distance
of the base of the ladder from the wall, after it is moved. Therefore,
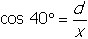 and
and
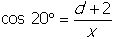 , so x cos 40° = d and
x cos 20° = d + 2. Then, x (cos 40° − cos 20°) = d
− (d + 2) = −2
, so x cos 40° = d and
x cos 20° = d + 2. Then, x (cos 40° − cos 20°) = d
− (d + 2) = −2
 x(−0.173648) = −2
x(−0.173648) = −2
 x ≈ 11.5 ft.
Correct Response: C. (Objective 0008) This problem can be represented by a diagram,
as shown below.
x ≈ 11.5 ft.
Correct Response: C. (Objective 0008) This problem can be represented by a diagram,
as shown below.
A ladder of length x leans against a vertical wall forming a twenty degree angle between the ladder
and the floor. The base of the ladder is a distance of d plus two feet from the wall. The ladder is
moved two feet closer to the wall to a distance of d where it now makes a forty degree angle between
the ladder and the floor.
In the diagram, x represents the length of the ladder, and d represents the distance
of the base of the ladder from the wall after it is moved. Therefore, cosine forty degrees equals d
over x and cosine twenty degrees equals start fraction numerator d plus two denominator x end fraction,
so x cosine forty degrees equals d and x cosine twenty degrees equals d
plus two. Then, x open parenthesis cosine forty degrees minus cosine twenty degrees close parenthesis
equals d minus open parenthesis d plus two close parenthesis equals negative two leads
to x open parenthesis negative zero point one seven three six four eight close parenthesis equals negative
two leads to x is approximately eleven point five feet.
Question 4
4. A balloon has the shape of a right cylinder of length L, with a hemisphere of radius r on each end,
as shown in the diagram below.
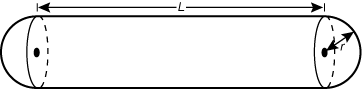
The length of the cylindrical part of the balloon, L, is 8 times the radius, r. Air
is added to the balloon, doubling the surface area while maintaining a similar shape. Which of the following
expressions represents the length of the larger balloon?
-
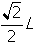 start fraction square root of 2 end root over two end fraction L
start fraction square root of 2 end root over two end fraction L
-
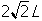 2 times square root of 2 end root L
2 times square root of 2 end root L
-
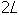 2L
2L
-
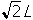 square root of 2 end root L
square root of 2 end root L
Answer to question 4
- Answer Enter to expand or collapse answer. Answer expanded
-
Correct Response: D. (Objective 0008) The surface area of the shape can be expressed as the sum of the surface areas of the two hemispheres (which is equivalent to one sphere) plus the surface area of the cylinder (without its bases): 4πr2 + 2πrL = 4πr2 + 2πr(8r) = 4πr2 + 16πr2 = 20πr2. Since the enlarged balloon is similar in shape to the original balloon, the length of the enlarged balloon (LE) is eight times its radius: LE = 8rE. The surface area of the enlarged balloon is double that of the original balloon, or 2 × 20πr2 = 40πr2; thus, the equation for the surface area of the enlarged balloon can be written as area = 4πrE2 + 2πrE(8rE) = 40πr2. This implies that 20πrE2 = 40πr2 ⇒ rE2 = 2r2 ⇒ rE = r√ 2 ⇒ 8rE = 8r√ 2 = √ 2 L.
Correct Response: D. (Objective 0008) The surface area of the shape can be expressed as the sum of the surface areas of the two hemispheres (which is equivalent to one sphere) plus the surface area of the cylinder (without its bases): 4 pi r squared plus 2pi rL equals 4pi r squared plus 2pi r left paren 8r right paren equals 4pi r squared plus 16pi rsquared equals 20pi rsquared. Since the enlarged balloon is similar in shape to the original balloon, the length of the enlarged balloon left paren LE right paren is eight times its radius: LE equals 8rE. The surface area of the enlarged balloon is double that of the original balloon, or 2 times 20pi r squared = 40pi r squared; thus, the equation for the surface area of the enlarged balloon can be written as area = 4pi rE squared plus 2pi rE left paren 8rE right paren equals 40pi r squared. This implies that 20pi rEsquared equals 40pi rsquared which becomes rE squared equals 2r squared which becomes rE equals r square root of 2 which becomes 8rE equals 8r square root of 2 equals square root of 2L
Question 5
5. What is the approximate area of the shaded semicircular arch shown below?
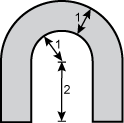
the inner border of the arch has a radius of one unit. the thickness of the arch from the inner border
to the outer border is also one unit.
- 5.6 square units
- 6.7 square units
- 7.1 square units
- 8.7 square units
Answer to question 5
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0008) The area of the arch can
be calculated as the sum of the areas of two rectangles plus the difference between half the area of
a large circle and half the area of a small circle:
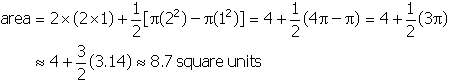 Correct Response: D. (Objective 0008) The area of the arch can be calculated as the
sum of the areas of two rectangles plus the difference between half the area of a large circle and half
the area of a small circle: area equals two times open parenthesis two times one close parenthesis plus
one half left bracket pi open parenthesis two squared close parenthesis minus pi open parenthesis one
squared close parenthesis right bracket equals four plus one half open parenthesis four pi minus pi
close parenthesis equals four plus one half open parenthesis three pi close parenthesis approximately
equal to four plus three halves open parenthesis three point one four close parenthesis approximately
equal to eight point seven square units.
Correct Response: D. (Objective 0008) The area of the arch can be calculated as the
sum of the areas of two rectangles plus the difference between half the area of a large circle and half
the area of a small circle: area equals two times open parenthesis two times one close parenthesis plus
one half left bracket pi open parenthesis two squared close parenthesis minus pi open parenthesis one
squared close parenthesis right bracket equals four plus one half open parenthesis four pi minus pi
close parenthesis equals four plus one half open parenthesis three pi close parenthesis approximately
equal to four plus three halves open parenthesis three point one four close parenthesis approximately
equal to eight point seven square units.
Question 6
6. A spherical ornament is packed in a box shaped like a cube. The interior dimensions of the box are
each equal to the diameter of the sphere. The spherical ornament takes up approximately what percent
of the space in the box?
- 52%
- 61%
- 70%
- 79%
Answer to question 6
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0008) The volume of a sphere with
radius r is
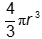 . Since
the interior dimensions of the box are each equal to the diameter of the sphere, the volume of the space
in the box is (2r)3 or 8r3. The ratio of the volumes is
. Since
the interior dimensions of the box are each equal to the diameter of the sphere, the volume of the space
in the box is (2r)3 or 8r3. The ratio of the volumes is
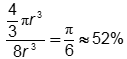 .
Correct Response: A. (Objective 0008) The volume of a sphere with radius r is four
thirds pi r cubed. Since the interior dimensions of the box are each equal to the diameter of the sphere,
the volume of the space in the box is open parenthesis two r close parenthesis cubed or eight r cubed.
The ratio of the volumes is the quantity four thirds pi r cubed over the quantity eight r cubed which
equals one sixth pi which approximately equals fifty two percent.
.
Correct Response: A. (Objective 0008) The volume of a sphere with radius r is four
thirds pi r cubed. Since the interior dimensions of the box are each equal to the diameter of the sphere,
the volume of the space in the box is open parenthesis two r close parenthesis cubed or eight r cubed.
The ratio of the volumes is the quantity four thirds pi r cubed over the quantity eight r cubed which
equals one sixth pi which approximately equals fifty two percent.
Question 7
7. If the measure of one of the interior angles of regular polygon P is three times the measure
of one of the exterior angles of a 9-sided regular polygon, how many sides does polygon P have?
- 6
- 8
- 10
- 12
Answer to question 7
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0009) The measure of an interior
angle of a regular polygon with n sides can be expressed as
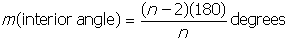 . The measure of an exterior angle of a polygon
with n sides can be expressed as the supplement of this, i.e.,
. The measure of an exterior angle of a polygon
with n sides can be expressed as the supplement of this, i.e.,
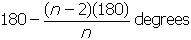 . Thus, the number of sides in polygon P
can be found by solving the equation
. Thus, the number of sides in polygon P
can be found by solving the equation
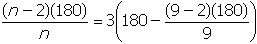 . So,
. So,
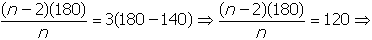 (n − 2)(180) = 120n. This implies that 60n = 360, and n =
6.
Correct Response: A. (Objective 0009) The measure of an interior angle of a regular
polygon with n sides can be expressed as m open parenthesis interior angle close parenthesis
equals start fraction numerator open parenthesis n minus two close parenthesis open parenthesis one
hundred and eighty close parenthesis denominator n end fraction degrees. The measure of an exterior
angle of a polygon with n sides can be expressed as the supplement of this, i.e., one hundred and eighty
minus start fraction numerator open parenthesis n minus two close parenthesis open parenthesis one hundred
and eighty close parenthesis denominator n end fraction degrees. Thus, the number of sides in polygon
P can be found by solving the equation start fraction numerator open parenthesis n minus two
close parenthesis open parenthesis one hundred and eighty close parenthesis denominator n end fraction
equals three open parenthesis one hundred and eighty minus start fraction numerator open parenthesis
nine minus two close parenthesis open parenthesis one hundred and eighty close parenthesis denominator
nine end fraction close parenthesis.
(n − 2)(180) = 120n. This implies that 60n = 360, and n =
6.
Correct Response: A. (Objective 0009) The measure of an interior angle of a regular
polygon with n sides can be expressed as m open parenthesis interior angle close parenthesis
equals start fraction numerator open parenthesis n minus two close parenthesis open parenthesis one
hundred and eighty close parenthesis denominator n end fraction degrees. The measure of an exterior
angle of a polygon with n sides can be expressed as the supplement of this, i.e., one hundred and eighty
minus start fraction numerator open parenthesis n minus two close parenthesis open parenthesis one hundred
and eighty close parenthesis denominator n end fraction degrees. Thus, the number of sides in polygon
P can be found by solving the equation start fraction numerator open parenthesis n minus two
close parenthesis open parenthesis one hundred and eighty close parenthesis denominator n end fraction
equals three open parenthesis one hundred and eighty minus start fraction numerator open parenthesis
nine minus two close parenthesis open parenthesis one hundred and eighty close parenthesis denominator
nine end fraction close parenthesis.
So, start fraction numerator open parenthesis n minus two close parenthesis open parenthesis one hundred
and eighty close parenthesis denominator n end fraction equals three open parenthesis one hundred and
eighty minus one hundred and forty close parenthesis leads to start fraction numerator open parenthesis
n minus two close parenthesis open parenthesis one hundred and eighty close parenthesis denominator
n end fraction equals one hundred and twenty leads to open parenthesis n minus two close parenthesis
open parenthesis one hundred and eighty close parenthesis equals one hundred and twenty n. This implies
that sixty n equals three hundred and sixty, and n equals six.
Question 8
8. A cylindrical hole 2
ft.
in diameter is drilled straight into the ground to make a well. If the dirt removed from the hole forms
a cone-shaped pile with a height of 6
ft.
and a diameter of 10
ft.
at the base, how deep is the well?
- 12
ft.
- 50
ft.
- 174
ft.
- 200
ft.
Answer to question 8
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0009) The volume of the cylindrical
hole can be calculated as Vcyl = πr2h = π(1)d,
where d represents the depth of the hole. The volume of the conical dirt pile can be calculated
as
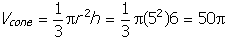 . Since Vcyl = Vcone,
πd = 50π, and d = 50
ft.
Correct Response: B. (Objective 0009) The volume of the cylindrical hole can be calculated
as volume of cylinder equals pi r squared h equals pi open parenthesis one close parenthesis d, where
d represents the depth of the hole. The volume of the conical dirt pile can be calculated as
v of cone equals one third pi r squared h equals one third pi open parenthesis five squared close parenthesis
six equals fifty pi. Since volume of a cylinder equals volume of a cone comma pi d equals fifty pi and
d equals fifty feet.
. Since Vcyl = Vcone,
πd = 50π, and d = 50
ft.
Correct Response: B. (Objective 0009) The volume of the cylindrical hole can be calculated
as volume of cylinder equals pi r squared h equals pi open parenthesis one close parenthesis d, where
d represents the depth of the hole. The volume of the conical dirt pile can be calculated as
v of cone equals one third pi r squared h equals one third pi open parenthesis five squared close parenthesis
six equals fifty pi. Since volume of a cylinder equals volume of a cone comma pi d equals fifty pi and
d equals fifty feet.
Question 9
9. If
 is a median and an altitude of Δtriangle XYZ, then Δtriangle XYZ must be:
is a median and an altitude of Δtriangle XYZ, then Δtriangle XYZ must be:
- equilateral.
- acute.
- isosceles.
- obtuse.
Answer to question 9
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0009) A median of a triangle is
a line segment from a vertex that intersects and bisects the opposite side. An altitude of a triangle
is a line segment from a vertex that is perpendicular to the opposite side. If the line segment from
a vertex both bisects and is perpendicular to the opposite side, the triangle may be equilateral, but
it must be isosceles.
Correct Response: C. (Objective 0009) A median of a triangle is a line segment from
a vertex that intersects and bisects the opposite side. An altitude of a triangle is a line segment
from a vertex that is perpendicular to the opposite side. If the line segment from a vertex both bisects
and is perpendicular to the opposite side, the triangle may be equilateral, but it must be
isosceles.
Question 10
10. Use the construction described below to answer the question that follows.
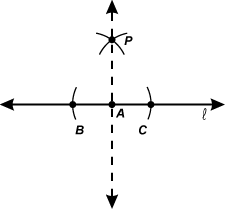
To construct a line perpendicular to a given line ℓ at point A:
1. From point A, construct arcs with the same radius intersecting line ℓ at points B
and C.
2. From each of points B and C, construct arcs with the same radius intersecting at
point P.
3. Draw line PAP A.
|
To prove that the construction shown results in line PA perpendicular to line ℓ, which
of the following congruent triangle theorems should be used?
- ASAA S A
- SSSS S S
- AASA A S
- HL H L
Answer to question 10
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0009) By construction, AB ≅ AC
and PB ≅ PC.
PC is congruent to itself by the reflexive property.
△PBA ≅ △PCA by SSS.
Correct Response: B. (Objective 0009) By construction, segment A B is congruent to
segment A C and segment PB is congruent to segment PC. Segment P A is congruent to itself by the reflexive property. Triangle
P B A is congruent to triangle P C A by S S S.
Question 11
11. The graphs of the polar equation r = 2cosθ and the rectangular equation x²
+ y² = 4 intersect at a point on the:
11. The graphs of the polar equation r equals two cosine theta and the rectangular equation x squared
plus y squared equals four intersect at a point on the:
- positive x-axis.
- negative x-axis.
- positive y-axis.
- negative y-axis.
Answer to question 11
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0010) The equation x2
+ y2 = 4 represents a circle centered at the origin with a radius of 2 units, so
this circle intersects the axes at (2, 0), (0, 2), (–2, 0), and (0, –2). Thus, in the equation
r = 2cosθ, either r = 2 or r = –2. If r = 2, cosθ
= 1 and θ = 0° or 360°, so the graph intersects the x-axis at (2, 0). If r
= –2, cosθ = –1 and θ = 180°. Negative radii reflect points over the origin,
so the graph again intersects the x-axis at (2, 0). Thus the two graphs intersect on the positive
x-axis.
Correct Response: A. (Objective 0010) The equation x squared plus y squared equals
four represents a circle centered at the origin with a radius of two units, so this circle intersects
the axes at ( 2 comma 0 ), ( 0 comma 2 ), ( negative 2 comma 0 ), and ( 0 comma negative 2 ). Thus,
in the equation r equals 2 cosine theta, either r equals 2 or r equals negative 2. If r equals 2, cosine
theta equals 1 and theta equals 0 degrees or three hundred sixty degrees, so the graph intersects the
x-axis at ( 2 comma 0 ). If r equals negative 2, cosine theta equals negative 1 and theta equals one
hundred eighty degrees. Negative radii reflect points over the origin, so the graph again intersects
the x-axis at ( 2 comma 0 ). Thus the two graphs intersect on the positive x-axis.
Question 12
12. Circle A in the coordinate plane has a diameter with coordinates (−negative 1, 7) and (7, 7). Circle B has a diameter with coordinates
(a, −negative 2) and
(3, −negative 2). If circle A
has an area that is 16 times that of circle B, what are the possible values of a?
- 2 or −negative 2
- 3 or 5
- 1 or −negative 1
- 1 or 5
Answer to question 12
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0010) The diameter of circle
A is 7 − (–1) = 8, so its radius is 4 units and its area is π(42) = 16π. Therefore,
the area of circle B must be π, and circle B must have a radius of 1. If the endpoint
of one diameter of circle B is at (3, −2) and the radius of B is 1 with a y-coordinate
of −2, the other endpoint must have the coordinates (1, −2) or (5, −2).
Correct Response: D. (Objective 0010) The diameter of circle A is 7 minus open parenthesis negative 1 close parenthesis equals eight, so its radius is four units and its area is pi open parenthesis four square
close parenthesis equals sixteen pi. Therefore, the area of circle B must be pi, and circle
B must have a radius of one. If the endpoint of one diameter of circle B is at open
parenthesis three comma negative two close parenthesis and the radius of B is one with a y-coordinate
of negative two, the other endpoint must have the coordinates open parenthesis one comma negative two
close parenthesis or open parenthesis five comma negative two close parenthesis.
Question 13
13. On a set of three-dimensional coordinate axes, a cube is located with its base coordinates at (0,
0, 0), (2, 0, 0), (0, 2, 0), and (2, 2, 0). The diagonals of the cube intersect at point M.
What is the distance of point M to a vertex of the cube?
-
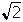 square root of 2
square root of 2
-
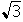 square root of 3
square root of 3
-
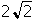 2 times the square root of 2
2 times the square root of 2
-
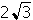 2 times the square root of 3
2 times the square root of 3
Answer to question 13
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0010) One of the diagonals has
as endpoints the coordinates (2, 0, 0) and (0, 2, 2). Using the distance formula, the length of this
diagonal is
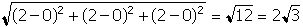 . Point M is the midpoint of the diagonal,
so the distance of M to a vertex is
. Point M is the midpoint of the diagonal,
so the distance of M to a vertex is
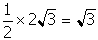 .
Correct Response: B. (Objective 0010) One of the diagonals has as endpoints the coordinates
open parenthesis two comma zero comma zero close parenthesis and open parenthesis zero comma two comma
two close parenthesis. Using the distance formula, the length of this diagonal is "start square root
open parenthesis two minus zero close parenthesis squared plus open parenthesis two minus zero close
parenthesis squared plus open parenthesis two minus zero close parenthesis squared end square root equals
square root of twelve equals two times the square root of three. Point M is the midpoint of
the diagonal, so the distance of M to a vertex is one half times two times the square root
of three equals the square root of three.
.
Correct Response: B. (Objective 0010) One of the diagonals has as endpoints the coordinates
open parenthesis two comma zero comma zero close parenthesis and open parenthesis zero comma two comma
two close parenthesis. Using the distance formula, the length of this diagonal is "start square root
open parenthesis two minus zero close parenthesis squared plus open parenthesis two minus zero close
parenthesis squared plus open parenthesis two minus zero close parenthesis squared end square root equals
square root of twelve equals two times the square root of three. Point M is the midpoint of
the diagonal, so the distance of M to a vertex is one half times two times the square root
of three equals the square root of three.
Question 14
14. Which of the following transformations reflects a figure in the coordinate plane over the line
y = x?
- (x, y) →right arrow (y, x)
- (x, y) →right arrow (y, −
negative x)
- (x, y) →right arrow (x, −
negative y)
- (x, y) →right arrow (− negative
x, − negative y)
Answer to question 14
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0010) The transformation (x,
y) → (y, x) interchanges the x- and y-coordinates, resulting in
the reflection of a point across the line y = x.
Correct Response: A. (Objective 0010) The transformation open parenthesis x comma
y close parenthesis right arrow open parenthesis y comma x close parenthesis interchanges the x-
and y-coordinates, resulting in the reflection of a point across the line y equals x.
Question 15
15. Use the triangle below to answer the question that follows.
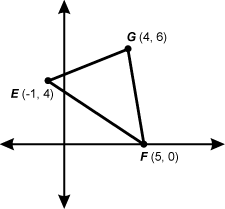
What is the equation of the perpendicular bisector of side EF E F of the triangle shown?
-
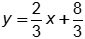
-
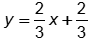
-
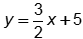
-
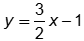
Answer to question 15
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0010) The perpendicular bisector
of side EF must go through the midpoint of side EF. Calculate the midpoint to get:
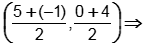 (2, 2). The slope of side EF is
(2, 2). The slope of side EF is
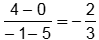 . The slope of a line perpendicular to
side EF must be the negative reciprocal of
. The slope of a line perpendicular to
side EF must be the negative reciprocal of
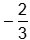 , or
, or
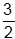 . Use the point-slope
form of the equation of a line to get:
. Use the point-slope
form of the equation of a line to get:
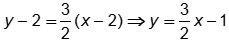 .
Correct Response: D. (Objective 0010) The perpendicular bisector of side E F must
go through the midpoint of side E F. Calculate the midpoint to get the quantity five plus negative one
over two comma the quantity zero plus four over two which becomes two comma two. The slope of side E
F is the quantity four minus zero over the quantity negative one minus five which equals negative two
thirds. The slope of a line perpendicular to side E F must be the negative reciprocal of negative two
thirds or three halves. Use the point-slope form of the equation of a line to get y minus two equals
three halves the quantity open parenthesis x minus two close parenthesis which yields y equals three
halves x minus one.
.
Correct Response: D. (Objective 0010) The perpendicular bisector of side E F must
go through the midpoint of side E F. Calculate the midpoint to get the quantity five plus negative one
over two comma the quantity zero plus four over two which becomes two comma two. The slope of side E
F is the quantity four minus zero over the quantity negative one minus five which equals negative two
thirds. The slope of a line perpendicular to side E F must be the negative reciprocal of negative two
thirds or three halves. Use the point-slope form of the equation of a line to get y minus two equals
three halves the quantity open parenthesis x minus two close parenthesis which yields y equals three
halves x minus one.
Question 16
16. Construction of a box plot to display data is particularly useful when:
- the number of data points is relatively small.
- a quick preliminary look at the shape of the data distribution is needed.
- comparisons are to be made between data sets of different sizes.
- identification of individual data points is desirable.
Answer to question 16
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0011) The advantages of box plots
are: the box plot highlights the important features of the data; the box plot makes it easier to focus
on the median, quartiles, and extreme values; and the box plot makes it easier to compare these features
to the same features in another data set by putting them on the same set of axes.
Correct Response: C. (Objective 0011) The advantages of box plots are: the box plot
highlights the important features of the data; the box plot makes it easier to focus on the median,
quartiles, and extreme values; and the box plot makes it easier to compare these features to the same
features in another data set by putting them on the same set of axes.
Question 17
17. Which of the following formats most clearly shows the overall shape and symmetry of a univariate
data distribution?
- histogram
- circle graph
- scatter plot
- line graph
Answer to question 17
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0011) A histogram consists of a
horizontal scale for data values, a vertical scale for frequencies, and bars that represent the various
data classes. Together the bars provide an effective visual representation of the shape and symmetry
of a univariate data distribution. A circle graph is an effective display of categorical data, a scatter
plot effectively displays bivariate data, and a line graph effectively displays time-series-dependent
data.
Correct Response: A. (Objective 0011) A histogram consists of a horizontal scale
for data values, a vertical scale for frequencies, and bars that represent the various data classes.
Together the bars provide an effective visual representation of the shape and symmetry of a univariate
data distribution. A circle graph is an effective display of categorical data, a scatter plot effectively
displays bivariate data, and a line graph effectively displays time-series-dependent data.
Question 18
18. Which of the following statements describes the data in the stem-and-leaf plot below?
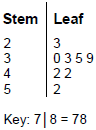
stem two leaf three. stem three leaf zero three five nine. stem four leaf two two. stem five leaf two.
key: stem seven leaf eight equals seventy eight.
- The mean and mode are equal and the median is smaller.
- The mean is greater than the median and smaller than the mode.
- The mean is less than the mode but greater than the median.
- The mean and median are equal and the mode is larger.
Answer to question 18
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0011) Here the mean is calculated
as
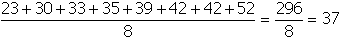 . The median is the middle value, which in this
case is the midpoint between 35 and 39, that is, 37. The mode is the most frequent value, 42. Thus,
the mean and median are equal and the mode is larger.
Correct Response: D. (Objective 0011) Here the mean is calculated as start fraction
numerator twenty three plus thirty plus thirty three plus thirty five plus thirty nine plus forty two
plus forty two plus fifty two denominator eight end fraction equals two hundred ninety six over eight
equals thirty seven. The median is the middle value, which in this case is the midpoint between 35 and
39, that is, 37. The mode is the most frequent value, 42. Thus, the mean and median are equal and the
mode is larger.
. The median is the middle value, which in this
case is the midpoint between 35 and 39, that is, 37. The mode is the most frequent value, 42. Thus,
the mean and median are equal and the mode is larger.
Correct Response: D. (Objective 0011) Here the mean is calculated as start fraction
numerator twenty three plus thirty plus thirty three plus thirty five plus thirty nine plus forty two
plus forty two plus fifty two denominator eight end fraction equals two hundred ninety six over eight
equals thirty seven. The median is the middle value, which in this case is the midpoint between 35 and
39, that is, 37. The mode is the most frequent value, 42. Thus, the mean and median are equal and the
mode is larger.
Question 19
19. The specifications for the composition of four candy mixtures are presented in the table below.
|
|
Mixture 1
|
Mixture 3
|
Mixture 3
|
Mixture 4
|
|
Mean
|
18%
|
24%
|
28%
|
32%
|
Standard
Deviation
|
8%
|
6%
|
4%
|
10%
|
% of Red
Jelly Beans
in Sample
|
30%
|
34%
|
18%
|
14%
|
A quality control manager takes a sample of each mixture and finds the percentage of red jelly beans
shown in the table. If the underlying distributions are assumed to be normally distributed, which mixture
is most likely to concern the manager?
- Mixture 1
- Mixture 2
- Mixture 3
- Mixture 4
Answer to question 19
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0011) If the underlying distribution
is normally distributed, approximately 95% of the samples taken should be within two standard deviations
of the mean. In the sample from Mixture 3, 95% of the samples should occur within the interval (0.2, 0.36); the sample of 18% falls outside this interval, raising questions about the percentage of red jelly beans in Mixture 3.
Correct Response: C. (Objective 0011) If the underlying distribution is normally
distributed, approximately ninety five percent of the samples taken should be within two standard deviations
of the mean. In the sample from Mixture 3, ninety five percent of the samples should occur within the
interval open parenthesis zero point two comma zero point three six close parenthesis; the sample of
eighteen percent falls outside this interval, raising questions about the percentage of red jelly beans
in Mixture 3.
Question 20
20. Meteorologists sampled tropical cyclones and found that there is a strong tendency for cyclones
to have greater wind speeds when the barometric pressure becomes very low as the cyclone approaches.
A scatterplot of readings plots the lowest pressure reading on the horizontal axis and the maximum wind
speed on the vertical axis for each cyclone in the sample. If the relationship is linear, which of the
following values could represent the correlation coefficient for this sample?
- 0.97
- 0.42
- –negative 0.36
- –negative 0.88
Answer to question 20
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0011) The correlation coefficient,
r, describes the strength of a linear relationship between two variables. The value of r
lies between –1 and 1. The closer r is to –1 or 1, the better a linear equation
fits the data. When the values of one variable decrease as the values of the other increase, then r
is negative. Since the correlation between wind speed and barometric pressure is strong, and since wind
speed increases as barometric pressure decreases, r must be close to –1. Thus, the best
response is –0.88.
Correct Response: D. (Objective 0011) The correlation coefficient, r, describes
the strength of a linear relationship between two variables. The value of r lies between negative
one and one. The closer r is to negative one or one, the better a linear equation fits the
data. When the values of one variable decrease as the values of the other increase, then r
is negative. Since the correlation between wind speed and barometric pressure is strong, and since wind
speed increases as barometric pressure decreases, r must be close to negative one. Thus, the
best response is negative zero point eight eight.
Question 21
21. If the two spinners below are spun simultaneously, what is the probability that the sum of the results
will be greater than or equal to 7?
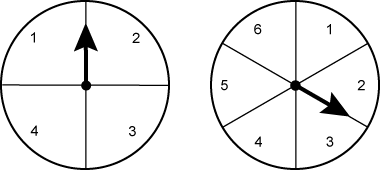
spinner on the left is divided into four equal sections labeled one, two, three, and four. Section one
is top left section and continues clockwise with section two, three, and four. there is an arm with
an arrow that is pointing up between section one and two on the spinner. spinner on the right is split
into six equal sections labeled one, two, three, four, five, and six. the one section is just to the
right of the middle top and and continues clockwise with sections two, three, four, five, and six. there
is an arm with an arrow that is in between sections two and three.
-
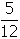
-
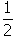
-
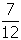
-
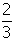
Answer to question 21
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0012) One method of solving this
problem is to make a table that shows all the possible outcomes when the two spinners are spun. This
is the sample space. The entry in each cell is the sum of the two spins.
Spinner
Value
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
From the table, note that 10 of the 24
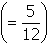 equally likely results produce a sum greater than or equal to 7.
equally likely results produce a sum greater than or equal to 7.
Question 22
22. The mean body length of beetles in a population is 7 mm. If body length in the population is normally
distributed, and 95% of the beetles have a body length between 6.2 and 7.8 mm, what is the best approximation
of the standard deviation of body length in the beetle population?
- 0.2 mm
- 0.4 mm
- 0.6 mm
- 0.8 mm
Answer to question 22
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0012) In a normally distributed
population, approximately 95% of the data points will be within 2 standard deviations of the mean of
the population. The interval within which the mean occurs here is 6.2–7.8, implying that the mean
of the population is 7 ± 2(0.4), where 0.4 is the standard deviation.
Correct Response: B. (Objective 0012) In a normally distributed population, approximately
ninety five percent of the data points will be within 2 standard deviations of the mean of the population.
The interval within which the mean occurs here is six point two through through seven point eight, implying
that the mean of the population is seven plus or minus two open parenthesis zero point four close parenthesis,
where zero point four is the standard deviation.
Question 23
23. A bag contains a large number of red and blue marbles. Fifty of the marbles are drawn randomly,
of which 40 are red and 10 are blue. These are replaced in the bag, and then 3 more marbles are drawn.
What is the approximate probability that exactly 2 of the 3 marbles drawn are red?
- 64%
- 51%
- 38%
- 13%
Answer to question 23
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0012) Since 40 of the 50 marbles
drawn initially are red, the best estimate of the percentage of red marbles in the bag is 80%. When
the 3 marbles are drawn, there are 3 possible outcomes that result in exactly 2 red marbles: RRB, RBR,
and BRR. The approximate probability desired is the sum of the probabilities of these 3 possible outcomes:
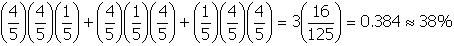 .
Correct Response: C. (Objective 0012) Since 40 of the 50 marbles drawn initially
are red, the best estimate of the percentage of red marbles in the bag is eighty percent. When the 3
marbles are drawn, there are 3 possible outcomes that result in exactly 2 red marbles: R R B, R B R,
and B R R. The approximate probability desired is the sum of the probabilities of these 3 possible outcomes:
open parenthesis four fifths close parenthesis open parenthesis four fifths close parenthesis open parenthesis
one fifth close parenthesis plus open parenthesis four fifths close parenthesis open parenthesis one
fifth close parenthesis open parenthesis four fifths close parenthesis plus open parenthesis one fifth
close parenthesis open parenthesis four fifths close parenthesis open parenthesis four fifths close
parenthesis equals three open parenthesis sixteen over one hundred and twenty five close parenthesis
equals zero point three eight four or approximately thirty eight percent.
.
Correct Response: C. (Objective 0012) Since 40 of the 50 marbles drawn initially
are red, the best estimate of the percentage of red marbles in the bag is eighty percent. When the 3
marbles are drawn, there are 3 possible outcomes that result in exactly 2 red marbles: R R B, R B R,
and B R R. The approximate probability desired is the sum of the probabilities of these 3 possible outcomes:
open parenthesis four fifths close parenthesis open parenthesis four fifths close parenthesis open parenthesis
one fifth close parenthesis plus open parenthesis four fifths close parenthesis open parenthesis one
fifth close parenthesis open parenthesis four fifths close parenthesis plus open parenthesis one fifth
close parenthesis open parenthesis four fifths close parenthesis open parenthesis four fifths close
parenthesis equals three open parenthesis sixteen over one hundred and twenty five close parenthesis
equals zero point three eight four or approximately thirty eight percent.
Question 24
24. When designing surveys, the reason for using random sampling techniques rather than other techniques
that may be more convenient is that random sampling will result in:
- larger sample sizes.
- smaller margins of error.
- less potential bias.
- higher levels of statistical significance.
Answer to question 24
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0012) Bias means that there are
consistent, repeated deviations of the sample statistic from the parameter being measured. Larger sample
sizes, smaller margins of error, and higher levels of statistical significance are all desirable in
analyzing statistical data, but the underlying reason for insisting on random techniques is to reduce
bias in the survey.
Correct Response: C. (Objective 0012) Bias means that there are consistent, repeated
deviations of the sample statistic from the parameter being measured. Larger sample sizes, smaller margins
of error, and higher levels of statistical significance are all desirable in analyzing statistical data,
but the underlying reason for insisting on random techniques is to reduce bias in the survey.
Question 25
25. There are four principal blood types: A, B, ABA
B, and O. Approximately 40% of the U.S. population has Type A blood. On a particular day,
a blood donation center needs 3 donors with Type A blood. Which of the following simulations should
be used to estimate, on average, the number of donors who need to be seen in order to obtain exactly
3 donors with Type A blood?
- Let heads on a coin represent Type A blood. Toss three coins and record the total number of heads.
Repeat 100 times.
- Let digits 0– through 3 represent
Type A blood. Read single-digit random numbers until three digits with values below four are read. Record
the number of random numbers read. Repeat 50 times.
- On a ten-sided die, let 1, 2, 3, and 4 represent Type A blood. Roll three ten-sided dice and record
the number of Type A results. Repeat 100 times.
- Use a spinner with 4 equal sections, one for each of the 4 blood types. Count the number of spins taken
until Type A has resulted three times. Repeat 50 times.
Answer to question 25
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0012) There are ten single digits,
0–9. Since 40% of the population has Type A blood, let the four digits 0, 1, 2, and 3 represent
these people. Read random one-digit numbers from a random number generator until three digits representing
Type A donors are found. The number of digits read in this trial represent the number of people seen
until three Type A donors are found. Repeat 50 times and average the 50 results to get an estimate of
the average number of people who need to be seen.
Correct Response: B. (Objective 0012) There are ten single digits, zero through nine.
Since forty percent of the population has Type A blood, let the four digits zero, one, two, and three
represent these people. Read random one-digit numbers from a random number generator until three digits
representing Type A donors are found. The number of digits read in this trial represent the number of
people seen until three Type A donors are found. Repeat fifty times and average the fifty results to
get an estimate of the average number of people who need to be seen.
Question 26
26. A clothing store tracks its inventory of red (R), green (G), and blue (B) clothing with the matrices
below.
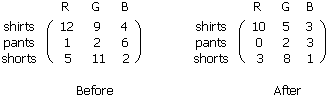
The matrix on the left shows the inventory before sales are recorded and the matrix on the right shows
the inventory after sales have been recorded. Which of the following categories of clothing shows the
greatest percent turnover?
There are two three by three matrices, one labeled before inventory and one labeled after inventory.
Both matrices have rows labeled, from the top down, as shirts, pants, and shorts. The columns in both
matrices are labeled, left to right, as red, green, and blue. The entries in the first row of the before
inventory are twelve, nine, and four; in the second row one, two, and six; and in the third row five,
eleven, and two. In the after matrix, the first row entries are ten, five, and three; the second row
entries are zero, two, and three; and in the third row, three, eight, and one.
- blue
- shorts
- red
- pants
Answer to question 26
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0013) To find the percent turnover,
find the number of pairs of pants in the inventory before sales were recorded: 1 + 2 + 6 = 9 and the
number of pairs of pants in the inventory after sales were recorded: 0 + 2 + 3 = 5. The turnover is
the difference, 4. To find the percent turnover, compare the turnover to the original inventory number:
4 ÷ 9 ≈ 44.4%. Comparing this figure to the results for blue (41.7%), shorts (33.3%), and
red (27.8%), the percent turnover for pants was the greatest.
Correct Response: D. (Objective 0013) To find the percent turnover, find the number
of pairs of pants in the inventory before sales were recorded: one plus two plus six equals nine and
the number of pairs of pants in the inventory after sales were recorded: zero plus two plus three equals
five. The turnover is the difference, four. To find the percent turnover, compare the turnover to the
original inventory number: four divided by nine approximately equals forty four point four percent.
Comparing this figure to the results for blue (forty one point seven percent), shorts (thirty three
point three percent), and red (twenty seven point eight percent), the percent turnover for pants was
the greatest.
Question 27
27. Set X consists of one element selected from set R = {1, 2}, one element from set
S = {3, 4, 5}, and one element from set T = {6, 7}. In how many ways can set X
be chosen to include either the 4, the 6, or both?
- 7
- 8
- 9
- 10
Answer to question 27
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0013) Ways of choosing set X that
meet the given criteria are {1, 3, 6}, {1, 4, 6}, {1, 4, 7}, {1, 5, 6}, {2, 3, 6}, {2, 4, 6}, {2, 4,
7}, and {2, 5, 6}. Alternatively, there are 2 × 3 × 2 = 12 possible sets, and only four
of these do not contain a 4 or a 6: {1, 3, 7}, {1, 5, 7}, {2, 3, 7}, and {2, 5, 7}.
Correct Response: B. (Objective 0013) Ways of choosing set X that meet the given
criteria are left brace one comma three comma six right brace, left brace one comma four comma six right
brace, left brace one comma four comma seven right brace, left brace one comma five comma six right
brace, left brace two comma three comma six right brace, left brace two comma four comma six right brace,
left brace two comma four comma seven right brace, and left brace two comma five comma six right brace.
Alternatively, there are two times three times two equals twelve possible sets, and only four of these
do not contain a four or a six: left brace one comma three comma seven right brace, left brace one comma
five comma seven right brace, left brace two comma three comma seven right brace, and left brace two
comma five comma seven right brace.
Question 28
28. Which of the following matrices is an identity matrix for matrix M below?
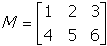
-
-
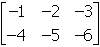
-
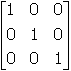
-
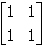
Answer to question 28
- Answer Enter to expand or collapse answer. Answer expanded
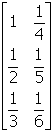
- Correct Response: C. (Objective 0013) If the product of a given
matrix M and matrix I is the original matrix M, I is an identity
matrix for M. In this case,
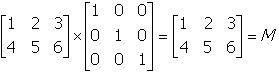 . Therefore,
. Therefore,
 is an identity matrix for matrix M. Note that
is an identity matrix for matrix M. Note that
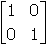 is also an identity matrix for M because
is also an identity matrix for M because
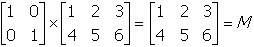 .
Correct Response: C. (Objective 0013) If the product of a given matrix M
and matrix I is the original matrix M, I is an identity matrix for M.
In this case, start two by three matrix first row first column one second column two third coulmn three.
second row first column four second column five third column six end matrix times start three by three
matrix first row first column one second column zero third column zero. second row first column zero
second column one third column zero. third row first column zero second column zero third column one
end matrix equals start two by three matrix first row first column one second column two third coulmn
three. second row first column four second column five third column six end matrix equals upper M. Therefore,
start three by three matrix first row first column one second column zero third column zero. second
row first column zero second column one third column zero. third row first column zero second column
zero third column one end matrix is an identity matrix for matrix M. Note that start two by
two matrix first row first column one second column zero. second row first column zero second column
one end matrix is also an identity matrix for M because start two by two matrix first row first
column one second column zero. second row first column zero second column one end matrix times start
two by three matrix first row first column one second column two third column three. second row first
column four second column five third column six end matrix equals start two by three matrix first row
first column one second column two third coulmn three. second row first column four second column five
third column six end matrix equals upper M.
.
Correct Response: C. (Objective 0013) If the product of a given matrix M
and matrix I is the original matrix M, I is an identity matrix for M.
In this case, start two by three matrix first row first column one second column two third coulmn three.
second row first column four second column five third column six end matrix times start three by three
matrix first row first column one second column zero third column zero. second row first column zero
second column one third column zero. third row first column zero second column zero third column one
end matrix equals start two by three matrix first row first column one second column two third coulmn
three. second row first column four second column five third column six end matrix equals upper M. Therefore,
start three by three matrix first row first column one second column zero third column zero. second
row first column zero second column one third column zero. third row first column zero second column
zero third column one end matrix is an identity matrix for matrix M. Note that start two by
two matrix first row first column one second column zero. second row first column zero second column
one end matrix is also an identity matrix for M because start two by two matrix first row first
column one second column zero. second row first column zero second column one end matrix times start
two by three matrix first row first column one second column two third column three. second row first
column four second column five third column six end matrix equals start two by three matrix first row
first column one second column two third coulmn three. second row first column four second column five
third column six end matrix equals upper M.
Question 29
29. Which of the following expressions represents the general relationship between the number of vertices,
v, edges, e, and faces, f, in a planar graph, such as the one shown below?

- e − v + f = 2
- v − f + e = 2
- e + v − f = 2
- v − e + f = 2
Answer to question 29
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0013) In solving this problem,
the examinee derives Euler's formula relating the number of vertices, edges, and faces of a planar graph
to each other. In this case, there are 8 vertices (intersections), 12 edges (line segments), and 6 faces
(including the outer unbounded face), numbers which are consistent with the equation v −
e + f = 2.
Correct Response: D. (Objective 0013) In solving this problem, the examinee derives
Euler's formula relating the number of vertices, edges, and faces of a planar graph to each other. In
this case, there are 8 vertices (intersections), 12 edges (line segments), and 6 faces (including the
outer unbounded face), numbers which are consistent with the equation v minus e plus f equals two.
Question 30
30. Use the Venn diagram below to answer the question that follows.
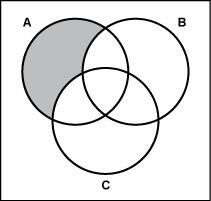
Which of the following expressions represents the shaded region in the Venn diagram shown?
-
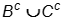
-
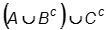
-
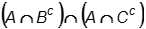
-
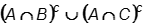
Answer to question 30
- Answer Enter to expand or collapse answer. Answer expanded
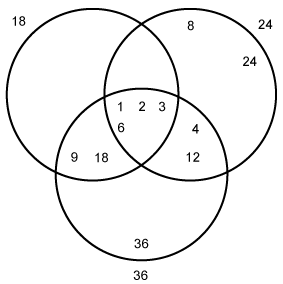
- Correct Response: C. (Objective 0013) The expression
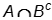 represents the set of things in A but not in B. Similarly,
represents the set of things in A but not in B. Similarly,
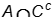 represents the set of things in A but not in C. The intersection of these sets is
the set of things in A which are neither in B nor in C. This statement describes
the given diagram.
Correct Response: C. (Objective 0013) The expression A intersection the complement
of B represents the set of things in A but not in B. Similarly, A intersection complement
of C represents the set of things in A but not in C. The intersection of these sets
is the set of things in A which are neither in B nor in C. This statement
describes the given diagram.
represents the set of things in A but not in C. The intersection of these sets is
the set of things in A which are neither in B nor in C. This statement describes
the given diagram.
Correct Response: C. (Objective 0013) The expression A intersection the complement
of B represents the set of things in A but not in B. Similarly, A intersection complement
of C represents the set of things in A but not in C. The intersection of these sets
is the set of things in A which are neither in B nor in C. This statement
describes the given diagram.
Question 31
31. Three faces of a rectangular prism have areas of 24, 32, and 48 square inches. If the lengths of
the sides are all integers, what is the volume of the prism?
- 96 in.396 inches cubed
- 192 in.3192 inches cubed
- 288 in.3288 inches cubed
- 384 in.3384 inches cubed
Answer to question 31
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0014) Knowledge of number theory
(factors) and geometry (volume) can be used to solve this problem. Possible side lengths of the 24-square-inch
face, the 32-square-inch face, and the 48-square-inch face are 1, 2, 3, 4, 6, 8, 12, and 24 inches;
1, 2, 4, 8, 16, and 32 inches; and 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48 inches, respectively. Start
with the 32-square-inch face, since that has the fewest factors: 32 cannot work, since neither of the
other two faces can have a side 32 inches long. If the dimensions of the 32-square-inch face are 16
× 2, then the dimensions of the prism must be 16 × 2, 16 × 3, and 2 × 3, but
there is not a 6-square-inch face. If the dimensions of the 32-square-inch face are 8 × 4, possible
dimensions of the prism are 8 × 4, 8 × 3, and 3 × 4 or 8 × 4, 8 × 6, and
4 × 6. Only the latter dimensions are consistent with face areas of 24, 32, and 48 square inches.
Thus, the volume of the prism is 8 × 6 × 4 = 192 cubic inches.
Correct Response: B. (Objective 0014) Knowledge of number theory (factors) and geometry
(volume) can be used to solve this problem. Possible side lengths of the 24-square-inch face, the 32-square-inch
face, and the 48-square-inch face are 1, 2, 3, 4, 6, 8, 12, and 24 inches; 1, 2, 4, 8, 16, and 32 inches;
and 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48 inches, respectively. Start with the 32-square-inch face, since
that has the fewest factors: 32 cannot work, since neither of the other two faces can have a side 32
inches long. If the dimensions of the 32-square-inch face are 16 times 2, then the dimensions of the
prism must be 16 times 2, 16 times 3, and 2 times 3, but there is not a 6-square-inch face. If the dimensions
of the 32-square-inch face are 8 times 4, possible dimensions of the prism are 8 times 4, 8 times 3,
and 3 times 4 or 8 times 4, 8 times 6, and 4 times 6. Only the latter dimensions are consistent with
face areas of 24, 32, and 48 square inches. Thus, the volume of the prism is 8 times 6 times 4 equals
192 cubic inches.
Question 32
32. Companies that sell life insurance set their premium rates using actuarial tables that provide data
on the life expectancies of people of different ages. This process of rate setting is based on which
of the following branches of mathematics?
- probability
- linear algebra
- calculus
- number theory
Answer to question 32
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0014) An actuarial table or life
table is a table that provides, for any given age, the probability that a person of that age will die
before their next birthday. It enables life insurance companies to calculate policy rates based on the
life expectancies of the people buying the insurance.
Correct Response: A. (Objective 0014) An actuarial table or life table is a table
that provides, for any given age, the probability that a person of that age will die before their next
birthday. It enables life insurance companies to calculate policy rates based on the life expectancies
of the people buying the insurance.
Question 33
33. Which of the following types of representations provides the most effective way to show the common
factors of three different numbers?
- number line
- circle graph
- Venn diagram
- function map
Answer to question 33
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0014) The Venn diagram below shows
all the factors of 18, 24, and 36, including their common factors. The factors 1, 2, 3, and 6, which
are common to all three numbers, are shown in the intersection of the three circles. The factors 9 and
18 that are common only to 18 and 36 show where those two circles intersect; and the factors 4 and 12
that are common to only 24 and 36 show where those two circles intersect. The factors 1, 2, 3, and 6,
which are common to all three numbers, are shown in the intersection of the three circles. The factors
9 and 18 that are common only to 18 and 36 show where those two circles intersect; and the factors 4
and 12 that are common to only 24 and 36 show where those two circles intersect.
 Correct Response: C. (Objective 0014) The Venn diagram below shows all the factors
of 18, 24, and 36, including their common factors. The factors 1, 2, 3, and 6, which are common to all
three numbers, are shown in the intersection of the three circles. The factors 9 and 18 that are common
only to 18 and 36 show where those two circles intersect; and the factors 4 and 12 that are common to
only 24 and 36 show where those two circles intersect. venn diagram showing the common factors of eighteen
twenty four and thirty six. Three overlapping circles with number inside specific parts to show the
relationship. The factors one, two, three, and six, which are common to all three numbers, are shown
in the intersection of the three circles. The factors nine and eighteen that are common only to eighteen
and thirty six show where those two circles intersect; and the factors four and twelve that are common
to only twenty four and thirty six show where those two circles intersect
Correct Response: C. (Objective 0014) The Venn diagram below shows all the factors
of 18, 24, and 36, including their common factors. The factors 1, 2, 3, and 6, which are common to all
three numbers, are shown in the intersection of the three circles. The factors 9 and 18 that are common
only to 18 and 36 show where those two circles intersect; and the factors 4 and 12 that are common to
only 24 and 36 show where those two circles intersect. venn diagram showing the common factors of eighteen
twenty four and thirty six. Three overlapping circles with number inside specific parts to show the
relationship. The factors one, two, three, and six, which are common to all three numbers, are shown
in the intersection of the three circles. The factors nine and eighteen that are common only to eighteen
and thirty six show where those two circles intersect; and the factors four and twelve that are common
to only twenty four and thirty six show where those two circles intersect
Question 34
34. Which of the following equations can be used to solve the problem below?
If one worker takes 3 hours to complete a job, and another worker takes 4 hours to complete a similar
job, how many hours, h, will it take the two workers to complete a job if they are working
together?
-
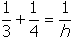
-
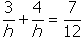
-
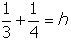
-
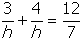
Answer to question 34
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0014) The number of jobs completed,
j, can be calculated as the product of the number of hours, h, worked, and the rate,
r, of work in jobs per hour, so j = h × r. In this case, the
total number of jobs completed by the workers together (j = 1) equals the sum of the work done
by each worker, or
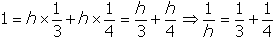 , which can then be solved for h. Alternatively,
reason directly that
, which can then be solved for h. Alternatively,
reason directly that
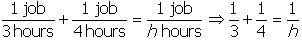 .
Correct Response: A. (Objective 0014) The number of jobs completed, j, can
be calculated as the product of the number of hours, h, worked, and the rate, r, of
work in jobs per hour, so j equals h multiplied by r. In this case, the total
number of jobs completed by the workers together open parenthesis j equals 1 close parenthesis
equals the sum of the work done by each worker, or one equals h times one third plus h times one fourth
equals h over three baseline plus h over four baseline leads to one over h baseline equals one third
plus one fourth, which can then be solved for h. Alternatively, reason directly that one job
over three hours baseline plus one job over four hours baseline equals one job over h hours baseline
leads to one third plus one fourth equals one over h.
.
Correct Response: A. (Objective 0014) The number of jobs completed, j, can
be calculated as the product of the number of hours, h, worked, and the rate, r, of
work in jobs per hour, so j equals h multiplied by r. In this case, the total
number of jobs completed by the workers together open parenthesis j equals 1 close parenthesis
equals the sum of the work done by each worker, or one equals h times one third plus h times one fourth
equals h over three baseline plus h over four baseline leads to one over h baseline equals one third
plus one fourth, which can then be solved for h. Alternatively, reason directly that one job
over three hours baseline plus one job over four hours baseline equals one job over h hours baseline
leads to one third plus one fourth equals one over h.
Question 35
35. Computers use logical operators based on the binary number system and combinations of AND and OR
circuits to perform the steps written into their software. Their language of logic is most directly
based on:
- Boolean algebra.
- the Binomial Theorem.
- modular arithmetic.
- Euler circuits.
Answer to question 35
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0014) George Boole (1815–1864)
believed that mathematics is a system of logical thought that could be used to show relationships between
classes of things. He devised a method of expressing statements symbolically and manipulating them algebraically.
Boolean logic can be applied to any statement that has exactly two outcomes: true/false, belonging/not
belonging, etc. The binary number system is used to express these outcomes through electrical flow (1
= true, belongs, etc.) or no flow (0 = false, does not belong, etc.) through the computer's circuits.
Correct Response: A. (Objective 0014) George Boole (eighteen fifteen to eighteen
sixty four) believed that mathematics is a system of logical thought that could be used to show relationships
between classes of things. He devised a method of expressing statements symbolically and manipulating
them algebraically. Boolean logic can be applied to any statement that has exactly two outcomes: true
or false, belonging or not belonging, etcetera. The binary number system is used to express these outcomes
through electrical flow (one equals true, belongs, etcetera) or no flow (zero equals false, does not
belong, etcetera) through the computer's circuits.
Question 36
36. Which of the following strategies would be most effective in promoting students' understanding and
retention of new vocabulary associated with a specific unit of study?
- using weekly quizzes to assess students' knowledge of newly introduced vocabulary
- having students look up definitions of new vocabulary in both a textbook glossary and a standard dictionary
- providing multiple opportunities for students to use new vocabulary in discussions and in their work
- encouraging students to enter new vocabulary in a personal dictionary of words they find interesting
or useful
Answer to question 36
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: C. (Objective 0015) Vocabulary knowledge is both
a key indicator and predictor of comprehension ability. Vocabulary knowledge and concept development
are closely interrelated; discipline-specific vocabulary development involves concept learning, and
concept learning supports academic vocabulary development. Vocabulary learning is an incremental process;
more exposures to and opportunities to use new vocabulary in context result in greater depth of understanding.
Providing students with multiple opportunities to use the vocabulary from a new unit of study in discussions
and in their writing promotes the students' vocabulary learning while simultaneously strengthening their
understanding of associated concepts.
Correct Response: C. (Objective 0015) Vocabulary knowledge is both a key indicator
and predictor of comprehension ability. Vocabulary knowledge and concept development are closely interrelated;
discipline-specific vocabulary development involves concept learning, and concept learning supports
academic vocabulary development. Vocabulary learning is an incremental process; more exposures to and
opportunities to use new vocabulary in context result in greater depth of understanding. Providing students
with multiple opportunities to use the vocabulary from a new unit of study in discussions and in their
writing promotes the students' vocabulary learning while simultaneously strengthening their understanding
of associated concepts.
Question 37
37. A student is reading a mathematics text and encounters a section that does not make sense to the
student. Which of the following strategies would be most appropriate for the student to use in this
situation to improve and repair reading comprehension?
- applying contextual analysis to deduce the meaning of any unfamiliar words encountered in the section
- increasing reading rate and fluency by skipping over the parts of the section that are most confusing
- identifying the topic sentences throughout the section and analyzing each of the sentences syntactically
- making connections between concepts previously read or learned and those presented in the section
Answer to question 37
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0015) As described, the student's
comprehension difficulty is limited to a particular section of the text and therefore the student has
understood the sections of text that preceded the problematic section. Typically, the concepts and information
presented in different sections of a mathematics text are related and are organized so that foundational
concepts and information are presented first. Making connections between concepts in the confusing section
and concepts previously learned in earlier sections is an effective metacognitive strategy for actively
constructing meaning during reading. The concepts previously presented are likely to provide relevant
background information to support comprehension of the difficult section.
Correct Response: D. (Objective 0015) As described, the student's comprehension difficulty
is limited to a particular section of the text and therefore the student has understood the sections
of text that preceded the problematic section. Typically, the concepts and information presented in
different sections of a mathematics text are related and are organized so that foundational concepts
and information are presented first. Making connections between concepts in the confusing section and
concepts previously learned in earlier sections is an effective metacognitive strategy for actively
constructing meaning during reading. The concepts previously presented are likely to provide relevant
background information to support comprehension of the difficult section.
Question 38
38. A mathematics teacher regularly conducts a "graphic walk" through a text prior to assigning the
text for reading. During the "walk," the teacher leads students in analyzing each graphic in the text
and noting in the text margins or on a sticky note what information the graphic conveys. Later, when
students read the text, the teacher has them look for statements or claims by the author that are supported
by the information in the graphic. The teacher's practice of conducting "graphic walks" supports students'
content-area reading development primarily by promoting their ability to:
- use graphic organizers to analyze a text's overall structure.
- summarize key information in a text without plagiarizing an author's words.
- make inferences about ideas or concepts described in a text.
- integrate and evaluate information presented in different formats in a text.
Answer to question 38
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: D. (Objective 0015) Graphics and text can present
similar information while emphasizing different details because of their varying formats. Helping students
make explicit connections between the information presented in the graphics and written discourse in
a text promotes their critical thinking and encourages them to integrate the information from diverse
formats as they read rather than treating graphics as extraneous information that can be ignored.
Correct Response: D. (Objective 0015) Graphics and text can present similar information
while emphasizing different details because of their varying formats. Helping students make explicit
connections between the information presented in the graphics and written discourse in a text promotes
their critical thinking and encourages them to integrate the information from diverse formats as they
read rather than treating graphics as extraneous information that can be ignored.
Question 39
39. Several students in a mathematics class demonstrate strong comprehension of the subject matter and
related terminology during class discussions. When called on to read aloud a section of a text in class,
they can read accurately and at an appropriate rate. However, these same students demonstrate little
comprehension of what they have read, even when they read a text silently. The mathematics teacher could
best address the content-area reading needs of these students by modeling and providing the students
with practice in which of the following components of reading as part of content-area lessons?
- applying morphological knowledge
- self-monitoring/questioning
- activating prior knowledge
- print processing/decoding
Answer to question 39
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: B. (Objective 0015) The students in this scenario
demonstrate proficiency in many key components and processes involved in reading—they have adequate
decoding and reading fluency skills, content-specific vocabulary knowledge, and background knowledge
of the subject matter. Yet, when they read a text orally or silently, they do not comprehend what they
are reading. Self-monitoring/questioning is a metacognitive strategy in which readers actively monitor
whether or not they understand what they are reading. If they encounter a problem, they immediately
seek to repair comprehension by self-questioning and rereading as necessary.
Correct Response: B. (Objective 0015) The students in this scenario demonstrate proficiency
in many key components and processes involved in reading—they have adequate decoding and reading
fluency skills, content-specific vocabulary knowledge, and background knowledge of the subject matter.
Yet, when they read a text orally or silently, they do not comprehend what they are reading. Self-monitoring/questioning
is a metacognitive strategy in which readers actively monitor whether or not they understand what they
are reading. If they encounter a problem, they immediately seek to repair comprehension by self-questioning
and rereading as necessary.
Question 40
40. A mathematics teacher would like to have students read a complex informational text that is closely
related to the current unit of study. However, the teacher is aware that the text is written above the
reading proficiency level of many students in the class. Which of the following approaches to using
the text would be most effective in both making the text's content accessible to all students and promoting
the students' content-area reading development?
- helping the students deconstruct the text's complex academic language and concepts during a whole-class
close reading of the text
- preparing a detailed written outline of the text's key ideas and details for the students to read and
study rather than assigning the original text
- selecting a different text that addresses more basic concepts and is written at a lower reading proficiency
level so that the students can read it independently
- providing a detailed oral preview of the text's key concepts, having the students read the text silently,
then providing an oral review of the concepts as reinforcement
Answer to question 40
- Answer Enter to expand or collapse answer. Answer expanded
- Correct Response: A. (Objective 0015) To promote students' college
and career readiness, content-area educators must prepare students to construct meaning from complex
discipline-specific texts. Reading research has shown that if students are "spoon-fed" the content of
complex texts, they never develop the skills and strategies necessary to grapple with complex texts
on their own. Instead of "spoon feeding," content-area teachers need to use a gradual release of responsibility
approach. Close reading involves reading and rereading a complex text, section by section, during which
the teacher models and provides students with opportunities to practice key content-area reading skills,
such as how to deconstruct syntactically complex sentences, use various word-learning strategies, and
apply relevant comprehension strategies to unlock the meaning and evaluate the significance of the text's
content.
Correct Response: A. (Objective 0015) To promote students' college and career readiness,
content-area educators must prepare students to construct meaning from complex discipline-specific texts.
Reading research has shown that if students are "spoon-fed" the content of complex texts, they never
develop the skills and strategies necessary to grapple with complex texts on their own. Instead of "spoon
feeding," content-area teachers need to use a gradual release of responsibility approach. Close reading
involves reading and rereading a complex text, section by section, during which the teacher models and
provides students with opportunities to practice key content-area reading skills, such as how to deconstruct
syntactically complex sentences, use various word-learning strategies, and apply relevant comprehension
strategies to unlock the meaning and evaluate the significance of the text's content.